Raising Bookworms: Getting Kids Reading for Pleasure and Empowerment by Emma Walton Hamilton
Room by Emma Donoghue
So look for those reviews coming up.
Friday, December 31, 2010
Out With A Bang Readathon Update
Raising Bookworms: Getting Kids Reading for Pleasure and Empowerment by Emma Walton Hamilton
Room by Emma Donoghue
So look for those reviews coming up.
Children's Math Book Review: Hamster Champs
Before I *finally* return this book to the shelf, I want to mention it. During our recent geometry classes, I read Hamster Champs
to the class after spending some time talking about degrees and doing a little exploration* with angles and protractors. In the story, three hamsters attempt a daring series of stunts, measuring degrees on a car ramp that sends them flying through the air. The cat promises not to chase them as long as he doesn't get bored. They taunt him with larger and larger angles until they eventually reach 180 degrees and speed away from him.
My geometry class, ages 8-11, loved the book...for two primary reasons, I think. First, they loved the taunting exchanges between the hamsters and the cat. Second, after having talked about angles in class, they understood some basics and could apply their knowledge to another "real" situation.
*Hmmm. I can't find notes about this on my blog. Hate it when I forget to write something from a lesson. I had the kids hold up two popsicle sticks and make acute, obtuse, straight, and right angles. We also looked at the vocabulary in Sir Cumference and the Great Knight of Angleland... the "'cute" steeply angled rooftops (acute angles) and the Mountains of Obtuse (obtuse angles
.)
Workbox activity: after learning about acute, obtuse, straight, and right angles, have children form them with popsicle sticks and draw models in their math journals. Read the two books mentioned here.
to the class after spending some time talking about degrees and doing a little exploration* with angles and protractors. In the story, three hamsters attempt a daring series of stunts, measuring degrees on a car ramp that sends them flying through the air. The cat promises not to chase them as long as he doesn't get bored. They taunt him with larger and larger angles until they eventually reach 180 degrees and speed away from him.My geometry class, ages 8-11, loved the book...for two primary reasons, I think. First, they loved the taunting exchanges between the hamsters and the cat. Second, after having talked about angles in class, they understood some basics and could apply their knowledge to another "real" situation.
*Hmmm. I can't find notes about this on my blog. Hate it when I forget to write something from a lesson. I had the kids hold up two popsicle sticks and make acute, obtuse, straight, and right angles. We also looked at the vocabulary in Sir Cumference and the Great Knight of Angleland... the "'cute" steeply angled rooftops (acute angles) and the Mountains of Obtuse (obtuse angles
.)Workbox activity: after learning about acute, obtuse, straight, and right angles, have children form them with popsicle sticks and draw models in their math journals. Read the two books mentioned here.
Science expected in 2011
Happy New Year 2011. Yes, it is a prime number. The probability that a number comparable to 2011 is a prime is 1/ln(2011) = 13%. So this coincidence proves global warming at a 87% confidence level. ;-)
The BBC has provided us with their perspective on science expectations for the year MMXI:
Extraterrestrial life
Some people are searching for ever more Earth-like planets that could be hospitable for life. The year 2010 has seen some probably valid discoveries as well as bogus reports but it's obvious that as the people are seeing newer and newer planets, the most Earth-like ones among them are becoming more Earth-like than their predecessors. ;-)
This is, of course, a fun business. But do you really believe that in a foreseeable future, people will find a planet such that they will be confident that there's life on it? I personally find it extremely unlikely. While the anthropic people may think that our vacuum of string theory is optimized to possess as many observers as possible, the empirical data suggest it's not the case.
See Why I am an extraterrestrial life skeptic.
It seems more sensible to me to believe that the vacuum is such that it "barely" allows an intelligent living planet to be born somewhere in a Hubble-scale spacetime volume of the Universe. You could say that it would be wasteful for Nature to produce many more living planets.
Needless to say, neither of the viewpoints - "life is common and easy" and "life is rare and hard" - can be supported by any real experimental data.
Private companies in space
For certain purposes, the commercial sector - companies around Richard Branson and others - is doing an immensely good job to keep us in space or at least "above the bulk of the atmosphere". There's no reason not to privatize these enterprises especially if they can be made profitable. Consumers may jump a little bit above the atmosphere - for the first time in their life - for $200,000.
This strategy remains limited because truly ambitious - as well as purely scientific - projects in the Cosmos are very expensive and probably not profitable in any practical sense. So I guess that the most ambitious projects in the space research will have to be funded by governments - and big governments - in a foreseeable future. Let's hope that people won't lose the desire to become important away from our beloved planet.
The LHC
Of course, I would spend much more time with the LHC but this blog has covered this gadget in quite some detail so I will avoid talkative summaries and speculations here.
In 2010, both major detectors of the collider - the ATLAS and the CMS - have collected about 47 inverse picobarns per detector and recorded about 43 inverse picobarns (92%). The data have largely confirmed the Standard Model. Hints of new physics remained inconclusive, to say the least. In fact, the LHC has already improved lower bounds on masses of most types of exotic particles and objects in a way that the Tevatron has no chance to match even if it were running for another decade: in this sense, the further running of the Tevatron became scientifically pointless.
Various signs of huge extra dimensions, anomalous light black holes, preons, new quark generations, W' bosons, and so on were excluded from a TeV or so. Most importantly, very light regions of supersymmetry have been pretty concisely excluded, including strongly interacting superpartners up to around 300 GeV.
The expected very light Higgs boson will take years to be discovered by the LHC; it's really the only type of really interesting physics in which the Tevatron could remain more powerful than the LHC.
In 2011, the European collider will run at 7 TeV (as in 2010) or 8 TeV (a tiny upgrade) and at luminosities that match or surpass the record of 2010 (which appeared at the very end of the 2010 run). It will collect about 1-5 inverse femtobarns per detector and it hasn't been decided whether the previous plan to stop the LHC for the whole year 2012 will be obeyed or abandoned.
The chances that the LHC will have enough data to see the lightest Higgs boson in 2011 are about 20%; the chances to see SUSY at the LHC in 2011 (which includes the fact that SUSY is less certain than the Higgs boson) are about 30% because SUSY is more "visible" to the LHC than a light Higgs boson. (The fact that particle physicists' subjective SUSY odds beat those of the Higgs was also revealed to the listeners on Ira Flatow's show after this article was written.) The Tevatron can't see SUSY in 2011 but its chances to reveal the Higgs in all of its data, including the old ones, are also about 20% for 2011.
In 2010, the LHC has seen some interesting "low-energy" QCD effects including quenched jets and other signs of the quark-gluon plasma and some not fully understood anomalies.
Progress in quantum computing
Quantum computers are possible when it comes to the physical principles but they remain a huge engineering challenge. Still, the year 2010 has encountered some progress in the people's ability to manipulate quantum bits, make them entangled, and keep them coherent. Several basic strategies are being tried and improved.
Additional progress of this kind may be expected in 2011. But don't expect quantum computers to break the Internet codes anytime during the next year.
Mars rovers and friends
The Spirit and Opportunity rovers landed on Mars in 2004 and were expected to survive for 90 our days (which are very close to Martian days) only. But they're still alive and kicking; the original life expectancy has been surpassed by a factor of twenty. This is an example of gadgets that just work.
I don't know if you have the same experience. But many devices are expected to die when they get old. However, in some cases, it's exactly the other way around. If a gadget such as a laptop has managed to work for 9 years, chances are that it can continue for another 9 years. Do you agree? ;-)
Once again, much of the Martian research is focused on the search for life. It's sexy for the laymen except that it's damn clear that there's no kind of life that would really be sexy for the laymen. Even if they managed to find some life forms, they would be some bacteria that could be visually indistinguishable from those on the Earth. I personally consider even such a modest possibility extremely unlikely.
Again, I can't prove it in any sense. But I do believe that certain numbers that determine the chance for life to emerge and survive decrease essentially exponentially as you deviate from the optimum zone. And Mars is deviated when it comes to many parameters, indeed. The planet is geometrically comparable to the Earth but when you count its "price" in terms of potency for life, it is just tiny relatively to the Earth.
In fact, privatizing Mars wouldn't be a bad idea and I think that the price should be low enough for some rich people to buy big portions of Mars, to say the least. Even the abundance of gold etc. on Mars is arguably smaller than on the Earth - given its much lower density, it shouldn't be surprising. So the commercial uses of Mars will almost certainly remain limited.
Theoretical physics
Many people will be attracted to phenomenology if the LHC results begin to be nontrivial. However, I wish pure theory to escape from the mud into which it has fallen in recent years - crackpottery similar to "gravity as the entropic force" and similar absurd non-quantitative nonsense that violates many fundamental insights we have made about the fundamental forces.
For example, two days ago, two new papers by Arkani-Hamed I and II appeared on the arXiv. They offer a manifestly local and cyclic-symmetric rewriting of the loop contributions to N=4 SYM theory's scattering amplitudes in terms of a single integral - just like in perturbative string theory that merges many different Feynman diagrams of the field-theoretical limit into a single topology.
The integral goes over some higher-dimensional Grassmannian and the integrand itself depends on objects that have a geometric interpretation in terms of areas of polytopes in various twistor or projective spaces and similar objects. Why do such objects appear and what's the general prescription to write the integrand for any amplitude? Is it analogous to the expectation value of a product of vertex operators on a Riemann surface in string theory?
I wish many more people tried to study these interesting things instead of the cheap pseudoscientific rubbish that the media like to write about.
The BBC has provided us with their perspective on science expectations for the year MMXI:A science news preview of 2011They chose five main topics:
- Hospitable planets
- Privatization of the cosmos
- The LHC: Higgs, SUSY
- Quantum computers
- Analyses of Mars & life
Extraterrestrial life
Some people are searching for ever more Earth-like planets that could be hospitable for life. The year 2010 has seen some probably valid discoveries as well as bogus reports but it's obvious that as the people are seeing newer and newer planets, the most Earth-like ones among them are becoming more Earth-like than their predecessors. ;-)
This is, of course, a fun business. But do you really believe that in a foreseeable future, people will find a planet such that they will be confident that there's life on it? I personally find it extremely unlikely. While the anthropic people may think that our vacuum of string theory is optimized to possess as many observers as possible, the empirical data suggest it's not the case.
See Why I am an extraterrestrial life skeptic.
It seems more sensible to me to believe that the vacuum is such that it "barely" allows an intelligent living planet to be born somewhere in a Hubble-scale spacetime volume of the Universe. You could say that it would be wasteful for Nature to produce many more living planets.
Needless to say, neither of the viewpoints - "life is common and easy" and "life is rare and hard" - can be supported by any real experimental data.
Private companies in space
For certain purposes, the commercial sector - companies around Richard Branson and others - is doing an immensely good job to keep us in space or at least "above the bulk of the atmosphere". There's no reason not to privatize these enterprises especially if they can be made profitable. Consumers may jump a little bit above the atmosphere - for the first time in their life - for $200,000.
This strategy remains limited because truly ambitious - as well as purely scientific - projects in the Cosmos are very expensive and probably not profitable in any practical sense. So I guess that the most ambitious projects in the space research will have to be funded by governments - and big governments - in a foreseeable future. Let's hope that people won't lose the desire to become important away from our beloved planet.
The LHC
Of course, I would spend much more time with the LHC but this blog has covered this gadget in quite some detail so I will avoid talkative summaries and speculations here.
In 2010, both major detectors of the collider - the ATLAS and the CMS - have collected about 47 inverse picobarns per detector and recorded about 43 inverse picobarns (92%). The data have largely confirmed the Standard Model. Hints of new physics remained inconclusive, to say the least. In fact, the LHC has already improved lower bounds on masses of most types of exotic particles and objects in a way that the Tevatron has no chance to match even if it were running for another decade: in this sense, the further running of the Tevatron became scientifically pointless.
Various signs of huge extra dimensions, anomalous light black holes, preons, new quark generations, W' bosons, and so on were excluded from a TeV or so. Most importantly, very light regions of supersymmetry have been pretty concisely excluded, including strongly interacting superpartners up to around 300 GeV.
The expected very light Higgs boson will take years to be discovered by the LHC; it's really the only type of really interesting physics in which the Tevatron could remain more powerful than the LHC.
In 2011, the European collider will run at 7 TeV (as in 2010) or 8 TeV (a tiny upgrade) and at luminosities that match or surpass the record of 2010 (which appeared at the very end of the 2010 run). It will collect about 1-5 inverse femtobarns per detector and it hasn't been decided whether the previous plan to stop the LHC for the whole year 2012 will be obeyed or abandoned.
The chances that the LHC will have enough data to see the lightest Higgs boson in 2011 are about 20%; the chances to see SUSY at the LHC in 2011 (which includes the fact that SUSY is less certain than the Higgs boson) are about 30% because SUSY is more "visible" to the LHC than a light Higgs boson. (The fact that particle physicists' subjective SUSY odds beat those of the Higgs was also revealed to the listeners on Ira Flatow's show after this article was written.) The Tevatron can't see SUSY in 2011 but its chances to reveal the Higgs in all of its data, including the old ones, are also about 20% for 2011.
In 2010, the LHC has seen some interesting "low-energy" QCD effects including quenched jets and other signs of the quark-gluon plasma and some not fully understood anomalies.
Progress in quantum computing
Quantum computers are possible when it comes to the physical principles but they remain a huge engineering challenge. Still, the year 2010 has encountered some progress in the people's ability to manipulate quantum bits, make them entangled, and keep them coherent. Several basic strategies are being tried and improved.
Additional progress of this kind may be expected in 2011. But don't expect quantum computers to break the Internet codes anytime during the next year.
Mars rovers and friends
The Spirit and Opportunity rovers landed on Mars in 2004 and were expected to survive for 90 our days (which are very close to Martian days) only. But they're still alive and kicking; the original life expectancy has been surpassed by a factor of twenty. This is an example of gadgets that just work.
I don't know if you have the same experience. But many devices are expected to die when they get old. However, in some cases, it's exactly the other way around. If a gadget such as a laptop has managed to work for 9 years, chances are that it can continue for another 9 years. Do you agree? ;-)
Once again, much of the Martian research is focused on the search for life. It's sexy for the laymen except that it's damn clear that there's no kind of life that would really be sexy for the laymen. Even if they managed to find some life forms, they would be some bacteria that could be visually indistinguishable from those on the Earth. I personally consider even such a modest possibility extremely unlikely.
Again, I can't prove it in any sense. But I do believe that certain numbers that determine the chance for life to emerge and survive decrease essentially exponentially as you deviate from the optimum zone. And Mars is deviated when it comes to many parameters, indeed. The planet is geometrically comparable to the Earth but when you count its "price" in terms of potency for life, it is just tiny relatively to the Earth.
In fact, privatizing Mars wouldn't be a bad idea and I think that the price should be low enough for some rich people to buy big portions of Mars, to say the least. Even the abundance of gold etc. on Mars is arguably smaller than on the Earth - given its much lower density, it shouldn't be surprising. So the commercial uses of Mars will almost certainly remain limited.
Theoretical physics
Many people will be attracted to phenomenology if the LHC results begin to be nontrivial. However, I wish pure theory to escape from the mud into which it has fallen in recent years - crackpottery similar to "gravity as the entropic force" and similar absurd non-quantitative nonsense that violates many fundamental insights we have made about the fundamental forces.
For example, two days ago, two new papers by Arkani-Hamed I and II appeared on the arXiv. They offer a manifestly local and cyclic-symmetric rewriting of the loop contributions to N=4 SYM theory's scattering amplitudes in terms of a single integral - just like in perturbative string theory that merges many different Feynman diagrams of the field-theoretical limit into a single topology.
The integral goes over some higher-dimensional Grassmannian and the integrand itself depends on objects that have a geometric interpretation in terms of areas of polytopes in various twistor or projective spaces and similar objects. Why do such objects appear and what's the general prescription to write the integrand for any amplitude? Is it analogous to the expectation value of a product of vertex operators on a Riemann surface in string theory?
I wish many more people tried to study these interesting things instead of the cheap pseudoscientific rubbish that the media like to write about.
Thursday, December 30, 2010
Chuck Norris in Czech commercials
Everyone in the Czech Republic knows Chuck Norris. In the 1980s, most Norris movies were actually smuggled into the country but he has already been well-known at that time. "Walker, Texas Ranger" was also among the first typical Western TV shows (thanks Mike) officially broadcast after the fall of communism.
Two months ago, T-Mobile Czech Republic, a Germany-based top cell-phone-service and satellite TV provider, ran a series of commercials that became hugely popular - millions of views at YouTube which is not bad for a commercial in a country of 10 million.
Norris was paid about $400,000 for the ads. His Czech colleague, actor Mr Valouch whom you will see, has received a free cell phone and became a new life-long Chuck Norris fan. ;-) While T-Mobile was most successful in the Christmas time, its competitors had creative ads, too. Vodafone has shot a few ads with Christmas trees that call each other while O2 has created origami paper cell phones.
The hostess says "Master!?" However, he refuses to kill the carp. What happens afterwards could be misinterpreted: Chuck Norris didn't faint; he just showed the floor who the boss was. ;-)
At the end of the ad, the husband of the hostess summarizes the situation: "Yup, yup: anyone may be sharp (tough) on TV." T-Mobile satellite TV offers a genuinely sharp image.
The comments under the YouTube video are funny - lots of new Chuck Norris facts are included.
"Hedgaaar - huh - huh. Mr Norris, now I will show you something." [Boom.] Chuck Norris doesn't spare anyone. T-Mobile will give you a free LCD TV after you purchase its three services.
"Sir, could you please take a photograph of us? It's the first time when my son bruslí [= is skating]." - "Bruce Lee? No. Chuck Norris." Chuck Norris won't give you everything for free. T-Mobile will give you a free digital frame if you buy one service.
"Look you, you will be impressed." - Chuck Norris won't give you anything for free. T-Mobile will give you a stylish netbook if you purchase two services.
Empower yourself at this time of advent. Buy prepaid credits at least for $20 and you will gain an advantage for every weekend. This Saturday and Sunday, the calls are free.
"Elia, forgive me." T-Mobile's satellite TV is wishing you truly powerful stories. [Onion.]
"Look, Ms Zuzana Noris[ová]. Isn't she a relative of yours?" - T-Mobile's satellite TV wishes you a star entertainment.
"Oh, I see, you are in Čakovice [Chuckville], Chuck (a neighborhood of Prague). I thought you got lost." Chuck Norris can never get lost. For the rest of us, T-Mobile brings a free Nokia phone with navigation forever for free.
"And just to be sure, where do you know him from?" - "Do you mean Norris? I thought that it was you who knew him."
"You must be impressed, Mr Norris, how many TV channels we have. News, sport, nature, nature, nature, nature, nature... If you were bored, I can switch the channel... I hope he's just sleeping." - That's too much to bear even for Chuck Norris. New T-Mobile satellite TV brings you hundreds of TV channels.
Knock, knock, knock. "Is everything alright, Mr Norris?" - "What's going on?" - "Mr Norris is having a bath." - "So I guess that the carp won't be too happy about that."
You may also play a special T-Mobile Flash game where you have to defeat Chuck Norris by your muscles, lasers, and arrow keys. At the beginning, Chuck Norris speaks in Czech with the Oklahoman accent or at least it's supposed to be this way haha. ;-)
Chuck Norris recently protested against climate treaties as a method to enslave America and create a world government.
See also Wall Street Journal
Chuck Norris holding a large, traditional Czech carp (WSJ blogs)
Two months ago, T-Mobile Czech Republic, a Germany-based top cell-phone-service and satellite TV provider, ran a series of commercials that became hugely popular - millions of views at YouTube which is not bad for a commercial in a country of 10 million.
Norris was paid about $400,000 for the ads. His Czech colleague, actor Mr Valouch whom you will see, has received a free cell phone and became a new life-long Chuck Norris fan. ;-) While T-Mobile was most successful in the Christmas time, its competitors had creative ads, too. Vodafone has shot a few ads with Christmas trees that call each other while O2 has created origami paper cell phones.
The hostess says "Master!?" However, he refuses to kill the carp. What happens afterwards could be misinterpreted: Chuck Norris didn't faint; he just showed the floor who the boss was. ;-)
At the end of the ad, the husband of the hostess summarizes the situation: "Yup, yup: anyone may be sharp (tough) on TV." T-Mobile satellite TV offers a genuinely sharp image.
The comments under the YouTube video are funny - lots of new Chuck Norris facts are included.
"Hedgaaar - huh - huh. Mr Norris, now I will show you something." [Boom.] Chuck Norris doesn't spare anyone. T-Mobile will give you a free LCD TV after you purchase its three services.
"Sir, could you please take a photograph of us? It's the first time when my son bruslí [= is skating]." - "Bruce Lee? No. Chuck Norris." Chuck Norris won't give you everything for free. T-Mobile will give you a free digital frame if you buy one service.
"Look you, you will be impressed." - Chuck Norris won't give you anything for free. T-Mobile will give you a stylish netbook if you purchase two services.
Empower yourself at this time of advent. Buy prepaid credits at least for $20 and you will gain an advantage for every weekend. This Saturday and Sunday, the calls are free.
"Elia, forgive me." T-Mobile's satellite TV is wishing you truly powerful stories. [Onion.]
"Look, Ms Zuzana Noris[ová]. Isn't she a relative of yours?" - T-Mobile's satellite TV wishes you a star entertainment.
"Oh, I see, you are in Čakovice [Chuckville], Chuck (a neighborhood of Prague). I thought you got lost." Chuck Norris can never get lost. For the rest of us, T-Mobile brings a free Nokia phone with navigation forever for free.
"And just to be sure, where do you know him from?" - "Do you mean Norris? I thought that it was you who knew him."
"You must be impressed, Mr Norris, how many TV channels we have. News, sport, nature, nature, nature, nature, nature... If you were bored, I can switch the channel... I hope he's just sleeping." - That's too much to bear even for Chuck Norris. New T-Mobile satellite TV brings you hundreds of TV channels.
Knock, knock, knock. "Is everything alright, Mr Norris?" - "What's going on?" - "Mr Norris is having a bath." - "So I guess that the carp won't be too happy about that."
You may also play a special T-Mobile Flash game where you have to defeat Chuck Norris by your muscles, lasers, and arrow keys. At the beginning, Chuck Norris speaks in Czech with the Oklahoman accent or at least it's supposed to be this way haha. ;-)
Chuck Norris recently protested against climate treaties as a method to enslave America and create a world government.
See also Wall Street Journal
Chuck Norris holding a large, traditional Czech carp (WSJ blogs)
Laughter May Increase Appetite
A hearty laugh and a moderate workout may have more in common than anyone thought.Both affect the appetite hormones in much the same way:
- When leptin goes down, it increases appetite
- When ghrelin goes up, it increases appetite
That is what typically happens after moderate exercise.
Leptin (from Greek, leptos, meaning thin) is a protein hormone that plays a key role in regulating energy intake and expenditure, including appetite and metabolism. Leptin acts on receptors in the hypothalamus of the brain where it inhibits appetite.
Ghrelin is a hormone that stimulates hunger. The name is based on its role as a growth hormone-releasing peptide, with reference to the root "ghre", meaning to grow. It is produced by the cells lining the fundus of the stomach and epsilon cells of the pancreas. It is considered the counterpart of the hormone leptin, produced by adipose tissue.
Twitter comments:
@LJaneTn Fat and Funny?
@doctorwhitecoat This explains why I'm always so hungry.
@scanman That explains why I eat too much when I party with friends.
Image source: Wikipedia, public domain.
Arsenic bacteria and climate disruption: a comparison
Four weeks ago, a press conference at NASA presented the claims by Ms Felisa Wolfe-Simon et al. who argued that during their searches in the Californian Mono Lake, they had found a bacterium that was able to replace phosphorus by arsenic (which is abundant in the lake - for natural reasons, which is why no one talks about this interesting lake) in its vital molecules, including the DNA that is normally built around a phosphate backbone. The paper eventually appeared in Science:A Bacterium That Can Grow by Using Arsenic Instead of Phosphorus (full text PDF)During and right after the press conference, your humble correspondent believed that the claims were likely to be true - partially because Ms Iron Lisa Wolfe-Simon was cute (I am not 100% immune against such things) and there was nothing "obviously wrong" with it. Arsenic is right beneath phosphorus in the periodic table and there was no reason why a random young passionate yet naive scientist and a former performance oboist couldn't have discovered such a new life strategy.
During the very press conference, critics argued that the arsenic compounds were much less stable than their phosphorus counterparts which made it impossible to use them in the DNA and other molecules and these critics turned out to be right.
Mr Steve Benner has pointed out that arsenate-based DNA would hydrolyze in water within 10 minutes (see also Mr Alex Bradley) - a claim that Wolfe-Simon et al. seem to agree with. That's not a good way to store the genetic information and indeed, building life around a similar unstable "memory" would be similar to building the Library of Alexandria - an eternal storage of human wisdom - with books out of sand. You know, this defect is pretty hard to "compensate".
Wolfe-Simon replied with some vague slogans about her claimed stability of As-DNA but her qualitative arguments are almost certainly wrong.
Ms Redfield vs Ms Wolfe-Simon
Now, when the paper in Science is available, it seems almost obvious that while the bacterium can survive in high concentrations of arsenic (unlike us), it doesn't actually use this element to grow. Instead, the bacteria used phosphorus from their ancestors and other biological contamination that wasn't under control. Ms Rosie Redfield (the lady with the rosie red hair on the picture above) offered the key viewpoint that had convinced me that there existed no evidence that arsenic was actually used by the bacteria anywhere.
By now, there is a widespread consensus that the paper hasn't demonstrated its key claim. As diverse people as your humble correspondent and people from the Real Climate blog agree. See also articles that mentioned Ms Redfield's points, a meaningful summary of the criticisms in the Slate, and MSNBC blogs.
Meanwhile, despite the growing perceived certainty that her paper is wrong, Iron Lisa remains an Iron Lady. Her paper has to be right, she says; the critics are wrong, only people who manage to pass through or fool the peer review process just like her have the right to think, and she will bring us new proofs - maybe even the E.T. himself will arrive to endorse her and her team (which includes physicist Paul Davies). ;-)
Also, she has never intended the paper to be hyped, we learn; she only attended the NASA press conference while she was boiling water for a coffee and someone told her to buy a new kettle in a mall - and it turned out to be the evil NASA people who forced her to participate at the press conference. :-)) (I am just popularizing her amusing claim about the lack of her desire to be very famous.)
What was the original evidence all about? Ms Wolfe-Simon claimed that the bacteria couldn't possibly survive with phosphorus only because she has had reduced the amount of phosphorus they could use - below the normal amount of phosphorus that the bacteria like to consume.
Now, this argument is of course bullshit - and because it was the only argument that arsenic was actually incorporated into the molecules of life, it instantly throws the whole paper to the trash bin. Why is it bullshit?
Well, if you normally drink 2 liters of water per day, it doesn't mean that you have to be a supernatural being or a dead body after a week when you could only drink 1 liter. The average consumption is not the same thing as the minimum consumption needed for survival. Chances are that arsenic wasn't included in a single viable molecule of life they studied. The new evidence is zero and the old theoretical evidence suggests that phosphorus can't be replaced.
It's clear that the paper shouldn't have been published - in a prestigious journal or otherwise - and NASA shouldn't have given it so much visibility because it was standing on one piece of evidence that had a self-evident bug in it. But if they couldn't have canceled the press conference, then during the press conference, they should have at least shown what was the actual evidence that the arsenic was incorporated - because viewers like me concluded that there had to be some real evidence and I feel cheated now.
However, on the other hand, NASA should be praised for having included a senior critic of Wolfe-Simon's conclusion - Steve Benner - at the press conference. He reviewed some old lore - a priori reasons to be skeptical. However, he didn't really address the positive evidence presented in the paper in any detail.
Lessons
The Real Climate Hockey Team compares the arsenic fiasco with the global warming hoax. You don't have to read their article - it's too talkative and redundant. The Real Climate people are junk scientists and they suck as communicators, too: they suck at so many levels.
They argue that the arsenic fiasco teaches us three lessons:
- Funding agencies deliberately pay studies that challenge the prevailing scientific opinion
- Scientists are also eager to overthrow the "consensus"
- Scientists like to distance themselves from flawed research because their credibility, and not funding, is at stake
Whether this message is consistent with the three partial lessons above is left to the reader. :-)
(I like Holdren's new term "climate disruption" because it allows one to accurately say that it doesn't exist - the claims about its existence are rubbish; one can't be so unambiguous about the terms "global warming" and "climate change" because some phenomena that could deserve these names exist - although they're something totally different than the catastrophes we often hear about.)
In principle, I agree with the three lessons. When science works, possibly revolutionary insights are preferred both by scientists and their sponsors. On the other hand, wrong revolutionary statements are more damaging which is why scientists distance themselves from extraordinary claims that are wrong according to the available evidence.
However, when institutionalized science doesn't work, it doesn't work. In the case of climate science which has become a totally corrupt field of science, the first two lessons above are pretty much right - for an interesting reason you will see - while the last lesson has to be modified a bit:
- In the context of climate science, funding agencies only pay for research that disagrees with the previous established insights of science, including the fact that there is absolutely nothing threatening about the ongoing or foreseeable climate change; studies that build on well-known facts or the proper scientific method are no longer funded
- Pretty much all scientists paid from such funds are indeed constantly trying to overthrow this consensus about the harmlessness and natural origin of climate change which is why they permanently invent ways to scare scientifically illiterate laymen and outsiders
- These corrupt pseudoscientists primarily care about their image among hundreds of similar corrupt pseudoscientists who decide about their careers, not among proper scientists or other honest and well-informed people, which is why they distance themselves from all the valuable research that analyzes how things actually work instead of how they could work to increase the funding
But I want to spend more time with some other, related lessons of the arsenic fiasco. First, Real Climate's lesson 3 says that what matters is the scientist's credibility and not funding. This is a very subtle claim. For ideal scientists such as your humble correspondent, this could be the case: an ideal scientist doesn't care about the funding too much. But the scientists in the real world of institutionalized science almost always care about the funding. It's just their job. They measure their credibility by the funding. It's completely preposterous to suggest otherwise.
Even Al Gore puts his money where his mouth is - as he often boasts - which means that other people have to put their mouths where Al Gore's money is, by the third Newton's law.
In disciplines whose organizational hierarchy works and hasn't been corrupted, the difference between "care for image" and "care for funding" is mostly immaterial because these two considerations produce very similar outcomes, or at least outcomes that are significantly and positively correlated. But in the climate science, it is not so.
There probably doesn't exist a single champion of the climate panic who could be said to have some significant scientific credibility left. As far as I know, pretty much all of them have been active players in the dishonest manipulations with the data, including ad hoc adjustments, cherry-picking, and overemphasis of possible conclusions of the research that could lead to an increase of the funding. Some of them have added blackmailing, harassment of inconvenient colleagues, and behind-the-scenes alliances with environmental terrorists to achieve their goals.
Those people don't care about their moral image - primarily because there are almost no powerful mechanisms in the society that would force them to care. In many corners, it is almost politically incorrect to insist that people such as Michael Mann who have fraudulently obtained the taxpayer money should return them, and/or be arrested. Scientific integrity should have much higher standards than the conventional human honesty - but in the context of climate science, even ordinary old-fashioned fraud involving stealing millions by producing untrue claims is not prosecuted in any way - so far. So the immoral bottom of the human society numerically dominates in the field of climate science.
Indeed, the main lesson of the arsenic fiasco is that the scientists and sponsors may be expected to have an inherent bias, trying to look for sensationally new claims that will make them famous. This is true both in the case of Ms Felisa Wolfe-Simon as well as in the case of the climate crusaders.
There is one additional lesson that hasn't been mentioned; I would call it lesson 4. Wolfe-Simon admitted that she was planning to find arsenic-consuming organisms from the very beginning; in her words, it was a directed search. Well, at the end, she did claim that her search was successful except that the research wasn't right. The same is happening in the case of the climate disruption. The lesson is:
4. If a researcher claims to have found something that he or she has planned and wanted to find from the very beginning, one should realize that such a researcher was biased and the probability that the evidence supporting such a predetermined conclusion is wrong, cherry-picked, or even fabricated substantially increases.Needless to say, virtually all of the officially funded "climate research" is based on the plan that the researchers want to find something shocking - some new kind of a threat or mechanism. That's surely the case of Alexander Ač and 149 other crackpots who are now funded by EUR 25 million "CzechGlobe" project of the European Union. For a person who is looking at the field from a distance, it's another reason to think that the claims about the climate disruption are analogous to the claims about the arsenic life forms.
Finally, let me add two more lessons of the arsenic story that is relevant for all of science, including climate science:
5. As long as a new scientific discovery remains incompatible with some previously established insights, i.e. until all the inconsistencies in the overall picture of science including the new discovery are cured, one has to appreciate the possibility that the empirical evidence supporting the new discovery is flawedAnd that's the memo.
6. Unless a rock solid proof of a new hypothesis has already been obtained, one should only decide about its validity after a fair comparison with alternative hypotheses; in this fair comparison, one shouldn't be biased in favor, or against, the alternatives that look more sensational
Burt Rutan on global warming
Burt Rutan is quite an amazing engineer who has designed original, efficient, unusual-looking, and record-breaking airplanes, some of which are not far from competing with NASA. Rutan has formed The Spaceship Company with Richard Branson.But he is also a global warming lecturer. Rutan is not just an ordinary global warming skeptic who becomes important by inventing a new, crisp expletive for CAGW. He is actually giving talks based on a 95-slide presentation of the whole topic:
Burt Rutan on CAGW v4.0:We appreciate Gene's viewpoints on science but one can say that Gene has been a scientist. It's comparably refreshing to see how an engineer who actually worked with engines :-) looks at the difference between science and engineering, especially when it comes to the responsibility and the frequency of errors.
PDF, PDF to HTML, PowerPoint
The July 2010 presentation reviews a lot of material we are familiar with and some of it may be new for us. Amusingly enough, page 37 of the presentation contains a picture taken from this blog - the collection of 11 graphs of energy flux predicted by models that happen to be beaten by just 1 reality that insisted on the opposite sign.
The dark green background - #003322 or #113322, I never remember which of them I actually chose haha - is a welcome side effect of making the background colors coincide on TRF. This side effect sometimes forces you to realize that a picture was taken from this blog, e.g. in the case of this graph of Lindzen and Choi. ;-)
There are lots of useful "philosophical" summaries in the talk - especially about the reduced reliability resulting from contrived and complicated models and from the desire to aggressively sell a product. I recommend you to spend some time with the presentation. But let me copy this conclusion:
“The Alarmist (scientist, journalist, politician etc.) chooses to huddle with other alarmists inside an echo chamber, attacking messengers who arrive, but spends no time to carefully inspect the data that forms his opinions, nor to notice the reporting of fraud”Thanks to Bill ZajcBurt Rutan, 2009
Wednesday, December 29, 2010
PAGING JASON KENNY! PAGING JASON KENNY! MULTI-CULTERS OUTA CONTROL. AGAIN
Blazing Cat Fur: Moderate Muslim Terrorists Foiled Again
Related tidbits:
if-muslims-were-treated-like-christians-in-america
wikileaks-us-embassy-pressured-danish paper not to reprint Mo-toons
somali-insurgents-obama-must-convert-to-islam-or-attacks-on-US-will-come
swedish-jihad-revelations
last but by no means least: Grond Zero Mosque Imam Feisal Abdul Rauf on speaking tour
Anticancer effect of "5 a day" fruit and vegetable servings is negligible
It is widely believed that cancer can be prevented by high intake of fruits and vegetables. However, inconsistent results from many studies have not been able to conclusively establish an inverse association between fruit and vegetable intake and overall cancer risk.
The European Prospective Investigation Into Cancer and Nutrition (EPIC) was a 9 year prospective study of nearly 500 000 Europeans. It concluded that the protective effect of eating fruit and vegetables is “very small” (J Natl Cancer Institute 2010).
Associations between reduced cancer risk and increased intake of total fruits and vegetables combined and total vegetables for the entire cohort were similar (200 g/d increased intake of fruits and vegetables combined, HR = 0.97); 100 g/d increased intake of total vegetables, HR = 0.98); intake of fruits showed a weaker inverse association (100 g/d increased intake of total fruits, HR = 0.99).
The reduced risk of cancer associated with high vegetable intake was restricted to women (HR = 0.98). Stratification by alcohol intake suggested a stronger reduction in risk in heavy drinkers and was confined to cancers caused by smoking and alcohol.
References:
Study finds that anticancer effect of “5 a day” is less than expected. BMJ, 2010.
Fruit and vegetable intake and overall cancer risk in the European Prospective Investigation into Cancer and Nutrition (EPIC). J Natl Cancer Inst. 2010 Apr 21;102(8):529-37. Epub 2010 Apr 6.
Fruit and vegetable intake and overall cancer risk in the European Prospective Investigation into Cancer and Nutrition (EPIC). J Natl Cancer Inst. 2010 Apr 21;102(8):529-37. Epub 2010 Apr 6.
President Obama has been smoking for 30 years and managed to quit - and so can you
The White House says President Obama has kicked the habit and stopped smoking. "It's been probably about nine months since he last smoked a cigarette," says Robert Gibbs, the President's press secretary, in an interview with CNN. Mr. Obama, like a lot of smokers, has quit before and started back up again. This time may be different. Gibbs says this is the longest he's known the President to go without a cigarette. He quit by chewing Nicorette gum and exercising a lot of will power.
References:
Stop smoking: Follow the President's example. CNN.
The globe cooled by 0.56 °C in four days
Throughout most of 2010, The UAH AMSU daily satellite temperature data have been showing almost each date to be the warmest one since 1998 or 1999. That was pretty much universally the case from January till the end of August.
However, even as recently as on December 16th, the day in 2010 was the warmest day with the same date since 1998. (The 1998 daily UAH data on that website only begin in August 1998 so the record-breaking warm H1 of 1998 is not included.)
This pattern has changed in the most recent week, however. On December 23rd, 2010, the global brightness near-surface temperature reached a local maximum of -16.75 °C. That was the fourth warmest reading since 1998 for that day after 2003, 2009, and 2006.
Things have gone in a different direction in the following four days. The most recent figure for the global brightness temperature is from December 27th, 2010, and it is -17.31 °C. This piece of data is the coolest number for a December 27th at least since 1998 (included).
The cooling between December 23rd and December 27th, 2010 is a whopping 0.56 °C. Pretty much all of 20th century global warming may have been erased within 4 days - the same time that Apollo 11 needed to get to the Moon, as correctly predicted by Jules Verne. ;-)
Did you notice that the "catastrophic" centennial global warming has disappeared in those four days? I don't think so because the observed centennial changes of the temperature have been zero for all practical (and a majority of impractical) purposes.
Because the end of December is near the annual minimum of the global temperature when the normal temperature is pretty much flat, almost none of those 0.56 °C can be attributed to the seasonal cycle. It's all about the random natural variability.
Despite these changes, GISS will probably declare 2010 as the warmest year but the other teams won't. Chances are that according to HadCRUT3, 2010 won't even be the second (or third) warmest year. Moreover, the cooler-than-normal temperatures are likely to continue (or escalate) in 2011.
Because La Nina is predicted to last at least through Spring 2011 (the most recent weekly 3.4 anomaly is -1.7 °C - it has strengthened again) and because its effect on the global temperature is delayed by 6 months or so, chances are that we will see cool global temperatures at least through Fall 2011. It is relatively plausible that 2011 will become one of the coolest years in the recent decade(s).
However, even as recently as on December 16th, the day in 2010 was the warmest day with the same date since 1998. (The 1998 daily UAH data on that website only begin in August 1998 so the record-breaking warm H1 of 1998 is not included.)
This pattern has changed in the most recent week, however. On December 23rd, 2010, the global brightness near-surface temperature reached a local maximum of -16.75 °C. That was the fourth warmest reading since 1998 for that day after 2003, 2009, and 2006.
Things have gone in a different direction in the following four days. The most recent figure for the global brightness temperature is from December 27th, 2010, and it is -17.31 °C. This piece of data is the coolest number for a December 27th at least since 1998 (included).
The cooling between December 23rd and December 27th, 2010 is a whopping 0.56 °C. Pretty much all of 20th century global warming may have been erased within 4 days - the same time that Apollo 11 needed to get to the Moon, as correctly predicted by Jules Verne. ;-)
Did you notice that the "catastrophic" centennial global warming has disappeared in those four days? I don't think so because the observed centennial changes of the temperature have been zero for all practical (and a majority of impractical) purposes.
Because the end of December is near the annual minimum of the global temperature when the normal temperature is pretty much flat, almost none of those 0.56 °C can be attributed to the seasonal cycle. It's all about the random natural variability.
Despite these changes, GISS will probably declare 2010 as the warmest year but the other teams won't. Chances are that according to HadCRUT3, 2010 won't even be the second (or third) warmest year. Moreover, the cooler-than-normal temperatures are likely to continue (or escalate) in 2011.
Because La Nina is predicted to last at least through Spring 2011 (the most recent weekly 3.4 anomaly is -1.7 °C - it has strengthened again) and because its effect on the global temperature is delayed by 6 months or so, chances are that we will see cool global temperatures at least through Fall 2011. It is relatively plausible that 2011 will become one of the coolest years in the recent decade(s).
Tuesday, December 28, 2010
Out With A Bang Readathon
I am not participating in the Debut Authors challenge and will be reading whatever books I want.
Click on the logo for more info or to sign up.
Let's Light the Writing Fire!
A lifetime ago, I worked as a high school, then middle school, language arts teacher. One of my primary jobs? Teaching writing. I used fun ideas. Somewhere between then and now, my enthusiasm and joy for teaching writing got lost. It's time to find it!
On the recommendation of one of my favorite teachers, I started reading Kids Have All the Write Stuff; Inspiring Your Children to Put Pencil to Paper
. (This book is available on Amazon, used, for the cost of shipping. I highly recommend it.) I'm newly inspired to make big changes in what we're doing with writing. I hope some of you join us!
My New Year's Goal: to excite my boys, ages 4 and 8, about writing!
Suggested Materials: the book has a lot of ideas, but I'm going to start by setting up some type of writing/art station (with tape, mini stapler, pens/pencils, art supplies) and providing each child with a writing box. If you use workboxes, you could continue with that format. I'm choosing to use something that looks different from our regular "school." I bought each boy a Sterilite 14" x 11" x 3 1/4" clip box
with snap-on lid.
Box Contents: the idea is for the contents to change on a regular basis, providing many varied opportunities for writing. The box could hold felt pens and paper. A variety of cards. Some stationary. Cut hearts. Stencils. You name it. Anything that will inspire children to write. And what can they write? Anything! Lists, menus, journals, comics, poetry, puzzles...ANYTHING! I want writing to be a playful part of daily life rather than always being associated with regular schoolwork. Here's what we'll start with...
Feelings Journals
My 8yo regularly journals as part of school. To change things up a bit I made some journal templates for each boy that reflect feelings. My 8yo will get to rank each day on a 1-10 scale and then describe why he choose that number. My 4yo gets to circle a face for the day--happy, sad, or in between--and dictate or use invented spelling to tell about his day. I'm having them do this at the table as I prepare dinner so that most of the day has passed before they write. Ideally, I'll join them and write in my own feelings journal.
Stationary Stuff
I have piles of old stationary (going back to my childhood--check out the photo!) that has pretty designs, pictures, etc. I'm going to put an assortment into each box along with stickers, envelopes and other correspondence-type material. Some of this will be "published" as we send them to friends and relatives. Others will be used as they play...making maps for their adventures, writing to each other, etc.
Future Contents
Mini-books of all kinds. Topic books...I'll demonstrate in a later blog entry. NCR/carbon copy paper. Adding machine tape. Tracing paper. Graph paper. Varied art materials.
I'm planning to change out the contents every few weeks. I'd love to hear your ideas for box materials. Anyone want to join our writing adventure? ;)
On the recommendation of one of my favorite teachers, I started reading Kids Have All the Write Stuff; Inspiring Your Children to Put Pencil to Paper
. (This book is available on Amazon, used, for the cost of shipping. I highly recommend it.) I'm newly inspired to make big changes in what we're doing with writing. I hope some of you join us!My New Year's Goal: to excite my boys, ages 4 and 8, about writing!
Suggested Materials: the book has a lot of ideas, but I'm going to start by setting up some type of writing/art station (with tape, mini stapler, pens/pencils, art supplies) and providing each child with a writing box. If you use workboxes, you could continue with that format. I'm choosing to use something that looks different from our regular "school." I bought each boy a Sterilite 14" x 11" x 3 1/4" clip box
with snap-on lid.
Box Contents: the idea is for the contents to change on a regular basis, providing many varied opportunities for writing. The box could hold felt pens and paper. A variety of cards. Some stationary. Cut hearts. Stencils. You name it. Anything that will inspire children to write. And what can they write? Anything! Lists, menus, journals, comics, poetry, puzzles...ANYTHING! I want writing to be a playful part of daily life rather than always being associated with regular schoolwork. Here's what we'll start with...Feelings Journals
My 8yo regularly journals as part of school. To change things up a bit I made some journal templates for each boy that reflect feelings. My 8yo will get to rank each day on a 1-10 scale and then describe why he choose that number. My 4yo gets to circle a face for the day--happy, sad, or in between--and dictate or use invented spelling to tell about his day. I'm having them do this at the table as I prepare dinner so that most of the day has passed before they write. Ideally, I'll join them and write in my own feelings journal.
I have piles of old stationary (going back to my childhood--check out the photo!) that has pretty designs, pictures, etc. I'm going to put an assortment into each box along with stickers, envelopes and other correspondence-type material. Some of this will be "published" as we send them to friends and relatives. Others will be used as they play...making maps for their adventures, writing to each other, etc.
Future Contents
Mini-books of all kinds. Topic books...I'll demonstrate in a later blog entry. NCR/carbon copy paper. Adding machine tape. Tracing paper. Graph paper. Varied art materials.
I'm planning to change out the contents every few weeks. I'd love to hear your ideas for box materials. Anyone want to join our writing adventure? ;)
Cleverest women are the heaviest drinkers, according to Telegraph newspaper
Not sure if this is the best choice for a headline... This is the original source: Education, alcohol use and abuse among young adults in Britain. Soc Sci Med. 2010 Jul.The findings come from a study carried out at the London School of Economics in which researchers tracked the lives of thousands of 34-year-old women and men, all born in the UK during the same week in 1970.
The report states: "The more educated women are, the more likely they are to drink alcohol on most days and to report having problems due to their drinking patterns.
"The better-educated appear to be the ones who engage the most in problematic patterns of alcohol consumption."
They may have more active social lives or work in male-dominated workplaces with a drinking culture. As girls, they may have grown up in middle-class families and seen their parents drink regularly.
According to the researchers, higher educational attainment is associated with increased odds of daily alcohol consumption and problem drinking. The relationship is stronger for females than males. Individuals who achieved high educational test scores in childhood are at a significantly higher risk of abusing alcohol across all dimensions.
References:
Cleverest women are the heaviest drinkers. Telegraph.
Cleverest women are the heaviest drinkers. Telegraph.
Education, alcohol use and abuse among young adults in Britain. Huerta MC, Borgonovi F. Soc Sci Med. 2010 Jul;71(1):143-51. Epub 2010 Mar 31.
Image source: Wikipedia.
Monday, December 27, 2010
Awesome Classical Music Deal!
Wish I'd known about this long ago. On Amazon, you can download *VERY INEXPENSIVE* MP3 albums of 99 Most Essential Masterpieces
for a variety of artists and categories: Mozart
, Handel
, Violin
, Piano
, Dvorak
, Schumann
, Beethoven
, Mendelssohn
, Liszt
, Tchaikovsky
, Bach
, Vivaldi
, Baroque
, Classical
and the list goes on and on. EACH album contains 99 songs. I bought the Handel album today as I've wanted to "try out" a sampling of Handel's music beyond The Messiah (a few of those songs are included, too.) I don't know if this is a temporary sale or a more permanent price. I just know it's really affordable.
This would be a perfect, cheap way to start a classical music library. I'll be using my album for homeschool since "more music" is on my "to do" list (or New Year's Resolution list); I plan to plug in a classical album and play it all morning as we're working. The 99 pieces/1 album I purchased equals over 4 hours of music. Music is vital to so many things...including learning math. Google "music improves math skills" for a sampling. ;)
P.S. If you're interested in the 99 Most Essential Christmas Masterpieces
, it's REALLY cheap!
Disclaimer: I have no affiliation with anything listed on this page. If you order from Amazon, all commissions go toward foster care through Grace and Hope at no additional cost to you. THANK YOU!
for a variety of artists and categories: Mozart, Handel, Violin, Piano, Dvorak, Schumann, Beethoven, Mendelssohn, Liszt, Tchaikovsky, Bach, Vivaldi, Baroque, Classical and the list goes on and on. EACH album contains 99 songs. I bought the Handel album today as I've wanted to "try out" a sampling of Handel's music beyond The Messiah (a few of those songs are included, too.) I don't know if this is a temporary sale or a more permanent price. I just know it's really affordable.This would be a perfect, cheap way to start a classical music library. I'll be using my album for homeschool since "more music" is on my "to do" list (or New Year's Resolution list); I plan to plug in a classical album and play it all morning as we're working. The 99 pieces/1 album I purchased equals over 4 hours of music. Music is vital to so many things...including learning math. Google "music improves math skills" for a sampling. ;)
P.S. If you're interested in the 99 Most Essential Christmas Masterpieces
, it's REALLY cheap! Disclaimer: I have no affiliation with anything listed on this page. If you order from Amazon, all commissions go toward foster care through Grace and Hope at no additional cost to you. THANK YOU!
Citibloc Fun
On the recommendation of friends, our two youngest boys received Citiblocs
for Christmas. Looking around on Christmas morning, however, you would have had a hard time figuring out who actually owned the blocks. My 20 and 16 yo daughters were the first to take the plunge. Here are some of the many creations from the past couple days...
for Christmas. Looking around on Christmas morning, however, you would have had a hard time figuring out who actually owned the blocks. My 20 and 16 yo daughters were the first to take the plunge. Here are some of the many creations from the past couple days...
Positive attitude and cheerfulness not related to college success
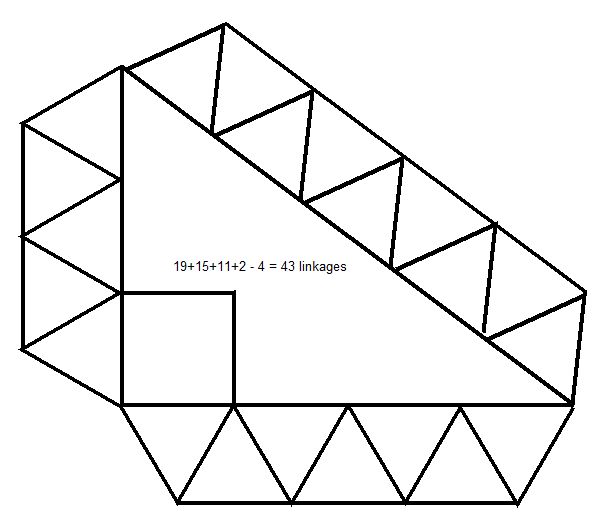
This study investigated the relation between positive affect and college success for undergraduate students matriculating at 21 colleges and universities in the United States. Positive affect — cheerfulness — was positively related to students’ self-rated academic abilities, self-predicted likelihoods of various college outcomes, self-stated major and academic-degree intentions, and self-reported subjective college outcomes, but negatively related to most objective college-success variables (e.g., cumulative college grade-point average) recorded by the institution of matriculation, and not related to objective college outcomes reported by the student.
Positive affect was thus associated with “positive illusions” about college-success variables.
References:
Positive Affect and College Success. Journal of Happiness Studies - SpringerLink Journal, 2010.
References:
Positive Affect and College Success. Journal of Happiness Studies - SpringerLink Journal, 2010.
Image source: OpenClipArt.org (public domain).
The big book of brain games: a puzzle
Ultimate spoiler:
A record solution that TRF reader bbzippo found a few years ago: 23 extra linkages, no intersections. Only previous record holders are discussed in detail here:
This solution of mine uses 31 extra edges or, if you allowed frictionless intersections and if you could shorten the lower left detour by one small triangle, it would use 29 extra edges. Go to the end of the article for comments why this is a valid solution.
Phil Gibbs' blog that I regularly read and learn from - and that actually doesn't irritate me in any way - posted a very cool Christmas puzzle from “The Big Book of Brain Games” by Ivan Moscovich. Most of the puzzles are claimed to be easy but puzzle number 331 is subtle and very interesting:
I recommend you to waste a few hours with drawing pictures whose faces have internal angles that are multiples of 30 degrees. It's useful because you will learn that one can waste a lot of time by drawing seemingly attractive structures if he or she makes a completely wrong assumption or too constraining an Ansatz about the solution. ;-)
An example of a solution attempt that doesn't work. Your humble correspondent drew many of them! :-)
It seems pretty clear to me that no solution of the kind that is describe in the previous big paragraph can exist. You must make the structure solid by thinking outside the box a little bit. :-) If it helps you, here is a Mathematica 7 code that allowed me to find my more nontrivial solution once I understood the broader concept that is actually promising:
To show my lemma, recall that the general linear combinations of the vectors t,u,v,w may be written as
It may only happen if this number four arises as 4+0+0+0 or 0+0+4+0 or 1+0+0+3 or 0+3+1+0 - all higher numbers are easily seen to exceed 4. Moreover, 1+3+0+0 and 0+0+1+3 are also forbidden because AB+CD would be nonzero (plus minus three). That proves that there are only 6 possible vectors and their 6 opposite vectors whose length is equal to one. In terms of the old basis, they were written as
This no-go theorem is an example of the fact that you may get stuck in drawing seemingly pretty pictures and you may hope that if you combine the flowers in a cleverer way than an hour ago, you will succeed. However, it can be shown that the whole infinite class of such pictures is ruled out.
The same thing holds in many other contexts. In particular, all people working on discrete theories of spacetime - or any quantum theory of gravity that is not equivalent to string theory - may spend lots of time (it's decades or centuries rather than hours in this case) by fabricating more convoluted models.
But it can be seen that there are no consistent non-stringy theories of quantum gravity. The latter statement and its proof are more complex than the example above - and the proof arguably demands a lot of knowledge from the readers - but the statement is equally true as the no-go theorem for solutions to the linkage problem whose angles are multiples of 30°.
You need to add a new player - internal angles that are not multiples of 30 degrees, in this case - to have a chance to find a solution. Then you enter a broader, different set of candidates - the counterpart of the string theory landscape - and in this set of candidates, which encourages you to study different issues than in the wrong class and to generalize them in different ways than before, you may actually construct correct and/or minimal solutions to your problem.
Spoilers: best solutions with 31 extra edges
The best solution available at this moment was found by your humble correspondenent by refining the Pythagorean idea. The Pythagorean solution was independently found by Phil Gibbs, Bill K, and Honza U. who was the first successful TRF reader to solve the challenge:
The solution uses the Pythagorean identity 3^2+4^2=5^2. The three "rigid bridge elements" contain 19, 15, 11 linkages, respectively, and 19+15+11+2-4 = 43 new linkages. The number doesn't change if you allow self-intersections (a point that was misinterpreted by Honza).
Mr/Ms Imho cannot be counted as a successful solver because he or she thought that you can erase the whole bridge elements and preserve just the 3+4+5 thin linkages surrounding the large 3-4-5 Pythagorean triangle (which would mean 12-2=10 extra linkages). Well, indeed, such a construction wouldn't be rigid at all and I hope that Mr/Ms Imho is not a professional architect. :-)
However, using the Mathematica code above, I found a more efficient solution that only uses 31 extra line segments:
or, if you allow frictionless intersections of the line segments, 29 extra linkages:
It is similar to the 3-4-5 Pythagorean triangle except that the catheti are not 3 and 4 but rather 2 and 3. You may complain that the hypotenuse is not an integer. Indeed, it's not: its length is sqrt(2^2+3^2) = sqrt(13).
However, one can create a rigid line segment of length sqrt(13) using the equilateral triangular truss, too. Draw a triangular truss that includes horizontal lines and the point (0,0). Make three steps to the East (right): the coordinate of the final point will be (3,0).
Now, make a step to the (almost) Northeast. You will add (1/2, sqrt(3)/2) to the coordinates of your point so the final point will be
The Mathematica program above, which has only searched through a set of sufficiently "small" solutions, has also found a solution with the hypotenuse equal to sqrt(39). In that solution, one has to use both directions of the triangular trusses on all three sides of the big triangle.
Exhaustive search: a proof of minimality
It's actually not hard to find the 29/31 solution above in a controlled, exhaustive search for economical solutions. Earlier in this text, I showed that there must exist internal angles that are not multiples of 30 degrees. Obviously, there must exist at least two such hinges where the internal angles not divisible by 30 degrees exist.
At least two such hinges are indirectly connected to the square by some linkages. Look at these two hinges. Of course, in the minimum setup, there will be exactly two such linkages.
The assumption in the previous sentence was proved to be wrong. The current most economical solution known to me - at the top of the article - depends on four hinges whose internal angles differ from multiples of 30 degrees. This fact invalidates the rest of the proof but it may still be interesting for you to read it.
To fix the angles of the square, the distance between these two linkages must be protected by an additional network of linkages - which will become the "hypertenuse" in the Pythagorean-based solutions. It's almost guaranteed that the minimal structure that preserves the distance is made out of a triangular truss.
Now, you may enumerate all the squared distances you may obtain from a triangular network. If you classify them by the number of "Northeast" steps, the allowed squared distances are:
Note that all of the squared lengths are integers. These are the allowed squared lengths of the "hypertenuse" block that preserves the distance between the two hinges. Now, the two hinges are connected to the square, so their coordinates have to differ by an integer combination of the vectors t,u,v,w mentioned previously.
Let's redo an exercise we did in a different basis. A general integral combination of the vectors t,u,v,w - the vector difference between the two hinges, as calculated from the block containing the square
Now, because the squared distances that can be supported by the "hypertenuse" blocks are integers, it follows that AD+BC has to vanish. Consequently, it can't be true that exactly three of the numbers A,B,C,D are nonzero: either 4 or 2 (or fewer) are nonzero. If 2 (or fewer) numbers among A,B,C,D are nonzero, we have either B=D=0 or A=C=0, which returns us to the Pythagorean numerology and 3-4-5 is the smallest solution (optimization of the 3-4-5 triangle may be discussed separately) , or A=B=0 or C=D=0 which are not allowed because the construction would only be attached to one of the sides of the square.
If all A,B,C,D are nonzero, which is the only room for solutions that may differ from the Pythagorean 3-4-5 concept, we have to check the combinations
That's why we have reduced the unknown yet promising solutions to the cases when all A,B,C,D are nonzero and expressed in terms of K,L as above. In the two inequivalent cases that make AD+BC vanish, namely K,L,K,-L and K,K,L,-L, the squared length of the vector (the sum of squares of A,B,C,D plus AB-CD) is equal to 2K^2+2L^2+-2KL or (3K^2+3K^2 or K^2+L^2).
The result must belong to the allowed list of squared lengths, 0, 1, 3, 4, 7, 9, 12, 13, 16, ... Clearly, the length 1 would only produce constructions with angles divisible by 30 degrees again which is no good, as proved at the beginning. Let's continue with the white list.
What about the squared length equal to 3, 7, 9, or 12?
The odd numbers can't be obtained as 2K^2+2L^2+-2KL because the latter is even. They can be written as K^2+L^2 or 3(K^2+L^2) but only if one of K,L vanishes... We want both K,L nonzero, as mentioned previously (because the construction would only be attached to one side of the square).
The smallest number of the form K^2+L^2 for positive integers K,L that is on the white list is 13 for K,L=2,3 or 3,2: numbers 2,5,8 are not on the white list. And 18 = 3^2+3^2 that would be just a little bit bigger is not on the white list, either.
The template 3(K^2+L^2) is clearly even less useful to create small solutions. The smallest allowed values of this tripled sum for positive integers K,L, namely 6,15,24..., are not on the white list, either. So far, K^2+L^2=9+4=13 is the only nontrivial small solution we found.
Finally, we must deal with the template 2(K^2+L^2+-KL); of course, the negative sign is better to produce smaller results. This can only match the even numbers on the white list, namely 4,12,16..., because it is even. K^2+L^2+-KL would have to be equal to 2,6,8... However, 2,6,8 can't be written in this form: 2,6 are equal to 2 modulo 4, but K^2+L^2+-KL can't be 2 mod 4. And 8 is also impossible for similar reasons.
So the only new small solution we found was one based on the hinges whose distance is sqrt(13).
Top intersecting solution
The assumption of just 2 vertices (hinges) that are not combinations of t,u,v,w is severely violated in the state-of-the-art best solutions. At the top, there is bbzippo's non-intersecting solution with 23 extra linkages.
Frictionless intersecting solutions can go down to incredible 15 extra linkages. This one is an example - a modified JollyJoker's structure:
Note that the original square with the pink vertices is rotated by 45 degrees. There are 3 additional - blue - vertices in the picture. Their 6 coordinates are constrained by 7 conditions on the length; this overdetermined system of conditions (by one) is just the right amount to fix the angle of the square with pink vertices.
The 7 distances that are fixed include the 3 vertical length-one distances from the adjacent pink vertices of the square; 2 length-one distances of the central light blue new point from the two dark blue new points on the sides; and 2 length-sqrt(3) distances of the upper blue points from the most distant pink vertices on the opposite side - that are realized by the di-triangle rhombuses.
This new solution brings you into an entirely new class of possibilities. Just add N vertices to the plane - outside the integer combinations of t,u,v,w - such that 2N+1 distances between these vertices (either between pairs of them, or between the vertices and arbitrary points in the "lattice" of integer combinations of t,u,v,w) belong to the white list (i.e. can be realized by inserting parts of triangular trusses).
Such a new template looks very general and it would be very time-consuming to look for all solutions, even pretty small ones, but I can still argue that even this general class actually doesn't exhaust all the possibilities. One could also "add the angles" etc.
A record solution that TRF reader bbzippo found a few years ago: 23 extra linkages, no intersections. Only previous record holders are discussed in detail here:
This solution of mine uses 31 extra edges or, if you allowed frictionless intersections and if you could shorten the lower left detour by one small triangle, it would use 29 extra edges. Go to the end of the article for comments why this is a valid solution.Phil Gibbs' blog that I regularly read and learn from - and that actually doesn't irritate me in any way - posted a very cool Christmas puzzle from “The Big Book of Brain Games” by Ivan Moscovich. Most of the puzzles are claimed to be easy but puzzle number 331 is subtle and very interesting:
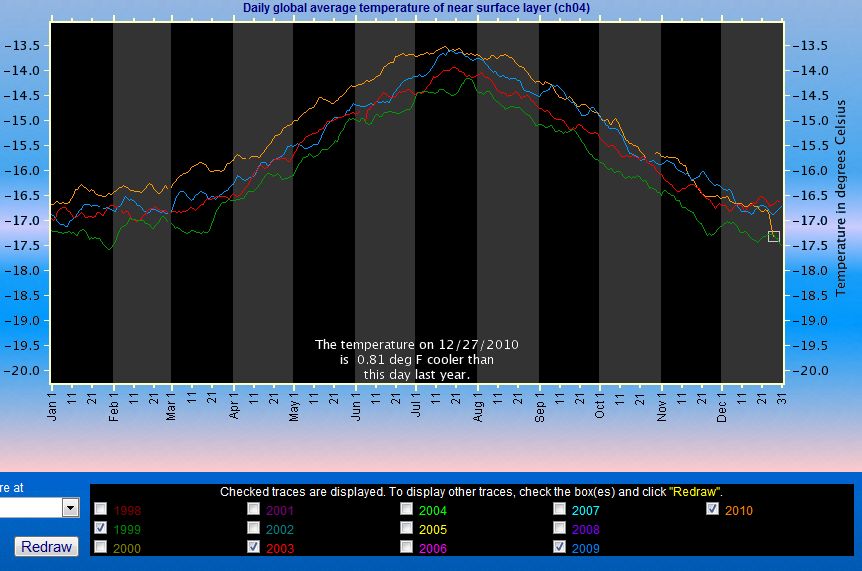
Draw a square consisting of four equally long connecting line segments hinged at the vertices. Such a structure may degenerate into a rhombus if you apply some pressure. How many additional interlinks of the same length must be supplemented to prohibit this excessive degree of freedom and to prevent the square from being tilted? The interlinks must belong to the same plane as the quad and each one may only be pegged to others at the endpoints.So far, I can't link to the original blog now because you would find a solution. The owner of the blog and his fastest reader found a solution with 43 extra linkages. After I was told what it was, your humble correspondent found a generalized solution of the same kind that only uses 29 extra linkages, if you allow me to draw frictionless intersections, or 31 extra linkages, if you don't.
I recommend you to waste a few hours with drawing pictures whose faces have internal angles that are multiples of 30 degrees. It's useful because you will learn that one can waste a lot of time by drawing seemingly attractive structures if he or she makes a completely wrong assumption or too constraining an Ansatz about the solution. ;-)
An example of a solution attempt that doesn't work. Your humble correspondent drew many of them! :-)
It seems pretty clear to me that no solution of the kind that is describe in the previous big paragraph can exist. You must make the structure solid by thinking outside the box a little bit. :-) If it helps you, here is a Mathematica 7 code that allowed me to find my more nontrivial solution once I understood the broader concept that is actually promising:
finds = {{0, 0, 0, 0, 0, 0, 0}};
(* next, separated line with input *)
Dynamic[{a, b, lenVsq, c, d, e, f}]
Dynamic[MatrixForm[finds]]
(* next, separated line with input *)
For[a = 1, a <= 7, a++,
For[b = -7, b <= 7, b++,
v = {a, 0} + b*{1/2, Sqrt[3]/2};
lenVsq = v[[1]]*v[[1]] + v[[2]]*v[[2]];
For[c = -5, c <= 5, c++,
For[d = -5, d <= 5, d++,
For[e = -5, e <= 5, e++,
For[f = -5, f <= 5, f++,
u = {d/2 + c, d*Sqrt[3]/2}
- {f*Sqrt[3]/2, f/2 + e};
lenUsq = u[[1]]*u[[1]] + u[[2]]*u[[2]];
finds =
If[(c*c + d*d)*(e*e + f*f) != 0 &&
Abs[lenUsq - lenVsq] < 0.00001,
finds~Join~{{a, b, lenVsq,
c, d, e, f}}, finds];
]
]
]
]
]
]
I guess that if you're not told the main idea, chances are that even the code above will be useless for you. Their "solution 43" as well as my "solution 29/31" have already been posted to the web but I won't give you coordinates before some of you try to solve it - and perhaps find an even more economical solution?
Bonus: a no-go theorem
I am sure that I was not the only one who got stuck for some time with tests of pictures like this one:
Well, JollyJoker is another victim because the picture above was offered by him.
Note that there is a whole class of pictures where all the linkages are either vertical, or horizontal, or have another azimuthal angle that is a multiple of 30 degrees. Correspondingly, all internal angles of all faces are multiples of 30 degrees as well - 30, 60, 90, 120, or 150 degrees.
With some help from TRF, it's straightforward to prove that no picture of this kind can be rigid.
First, use (0,0), (1,0), (0,1), (1,1) for the vertices of the square. If all edges have one of the allowed azimuthal angles mentioned above - 0, 30, 60, 90, 120, or 150 degrees (or the opposite-direction edges whose azimuthal angle differs by 180 degrees), then all vertices or hinges indirectly connected to the square have coordinates that are integer linear combinations of the following four vectors:t = (1, 0)Note that the nontrivial numbers are, up to the last sign, sines and cosines of 30 or 60 degrees. However, if you have a collection of points whose coordinates are
u = (1/2, sqrt(3)/2)
v = (0, 1)
w = (sqrt(3)/2, -1/2)
at + bu + cv + dw,then you can see that both coordinates of the points are integer combinations of 1/2 and sqrt(3)/2. However, you may deform the picture by preserving vectors t,u and rotating v,w into v',w':
a, b, c, d are integers,
v' = (sin(phi), cos(phi))All edges whose length was equal to 1 in the old diagram - composed of points with coordinates point - have to have the length 1 in the new diagram composed of points with coordinates point'. That's because
w' = (sin(120°+phi), cos(120°+phi))
point' = at + bu + cv' + dw',
a, b, c, d are integers.
t, u, t-u; -t, -u, -t+u;are the only integer combinations of vectors t,u,v,w whose length is (or was) exactly equal to one (see below). However, if you replace v,w by v',w' in the expressions above, it's still true that all the vectors will have length equal to one. That proves that the diagram may be tilted.
v, w, v+w; -v, -w, -v-w
To show my lemma, recall that the general linear combinations of the vectors t,u,v,w may be written as
{ (A+B sqrt(3))/2, (C+D sqrt(3))/2 }Four times the squared length of this vector should be equal to 4 but it is
+ A2 + 3B2 +where A,B,C,D are integers. This can only be equal to 4 if (AB+CD) vanishes - it's the coefficient of the square root of three, an irrational number that can't cancel against others because of the integrality of the coefficients. Moreover, the four positive terms on the first two lines have to add up to four.
+ C2 + 3D2 +
2 sqrt(3) (AB+CD)
It may only happen if this number four arises as 4+0+0+0 or 0+0+4+0 or 1+0+0+3 or 0+3+1+0 - all higher numbers are easily seen to exceed 4. Moreover, 1+3+0+0 and 0+0+1+3 are also forbidden because AB+CD would be nonzero (plus minus three). That proves that there are only 6 possible vectors and their 6 opposite vectors whose length is equal to one. In terms of the old basis, they were written as
t, u, t-u; -t, -u, -t+u;You see that the combinations of t,u are decoupled from the combinations of v,w, so you may rotate v,w separately from t,u (that you may keep fixed, for example), and it won't break any of the linkages because all linkages that existed will continue to have length equal to one.
v, w, v+w; -v, -w, -v-w
This no-go theorem is an example of the fact that you may get stuck in drawing seemingly pretty pictures and you may hope that if you combine the flowers in a cleverer way than an hour ago, you will succeed. However, it can be shown that the whole infinite class of such pictures is ruled out.
The same thing holds in many other contexts. In particular, all people working on discrete theories of spacetime - or any quantum theory of gravity that is not equivalent to string theory - may spend lots of time (it's decades or centuries rather than hours in this case) by fabricating more convoluted models.
But it can be seen that there are no consistent non-stringy theories of quantum gravity. The latter statement and its proof are more complex than the example above - and the proof arguably demands a lot of knowledge from the readers - but the statement is equally true as the no-go theorem for solutions to the linkage problem whose angles are multiples of 30°.
You need to add a new player - internal angles that are not multiples of 30 degrees, in this case - to have a chance to find a solution. Then you enter a broader, different set of candidates - the counterpart of the string theory landscape - and in this set of candidates, which encourages you to study different issues than in the wrong class and to generalize them in different ways than before, you may actually construct correct and/or minimal solutions to your problem.
Spoilers: best solutions with 31 extra edges
The best solution available at this moment was found by your humble correspondenent by refining the Pythagorean idea. The Pythagorean solution was independently found by Phil Gibbs, Bill K, and Honza U. who was the first successful TRF reader to solve the challenge:
The solution uses the Pythagorean identity 3^2+4^2=5^2. The three "rigid bridge elements" contain 19, 15, 11 linkages, respectively, and 19+15+11+2-4 = 43 new linkages. The number doesn't change if you allow self-intersections (a point that was misinterpreted by Honza).
Mr/Ms Imho cannot be counted as a successful solver because he or she thought that you can erase the whole bridge elements and preserve just the 3+4+5 thin linkages surrounding the large 3-4-5 Pythagorean triangle (which would mean 12-2=10 extra linkages). Well, indeed, such a construction wouldn't be rigid at all and I hope that Mr/Ms Imho is not a professional architect. :-)
However, using the Mathematica code above, I found a more efficient solution that only uses 31 extra line segments:
or, if you allow frictionless intersections of the line segments, 29 extra linkages:
It is similar to the 3-4-5 Pythagorean triangle except that the catheti are not 3 and 4 but rather 2 and 3. You may complain that the hypotenuse is not an integer. Indeed, it's not: its length is sqrt(2^2+3^2) = sqrt(13).
However, one can create a rigid line segment of length sqrt(13) using the equilateral triangular truss, too. Draw a triangular truss that includes horizontal lines and the point (0,0). Make three steps to the East (right): the coordinate of the final point will be (3,0).
Now, make a step to the (almost) Northeast. You will add (1/2, sqrt(3)/2) to the coordinates of your point so the final point will be
(3.5, sqrt(3)/2)The squared length of this vector - the distance between the two points of the triangular truss - equals
3.52 + 3/4 = 12.25 + 0.75 = 13just like previously. So three pieces of the triangular bridge construction may be connected just like in the case of the 3-4-5 Pythagorean triangle and the right angle of the square is ensured in this way.
The Mathematica program above, which has only searched through a set of sufficiently "small" solutions, has also found a solution with the hypotenuse equal to sqrt(39). In that solution, one has to use both directions of the triangular trusses on all three sides of the big triangle.
Exhaustive search: a proof of minimality
It's actually not hard to find the 29/31 solution above in a controlled, exhaustive search for economical solutions. Earlier in this text, I showed that there must exist internal angles that are not multiples of 30 degrees. Obviously, there must exist at least two such hinges where the internal angles not divisible by 30 degrees exist.
At least two such hinges are indirectly connected to the square by some linkages. Look at these two hinges. Of course, in the minimum setup, there will be exactly two such linkages.
The assumption in the previous sentence was proved to be wrong. The current most economical solution known to me - at the top of the article - depends on four hinges whose internal angles differ from multiples of 30 degrees. This fact invalidates the rest of the proof but it may still be interesting for you to read it.
To fix the angles of the square, the distance between these two linkages must be protected by an additional network of linkages - which will become the "hypertenuse" in the Pythagorean-based solutions. It's almost guaranteed that the minimal structure that preserves the distance is made out of a triangular truss.
Now, you may enumerate all the squared distances you may obtain from a triangular network. If you classify them by the number of "Northeast" steps, the allowed squared distances are:
0 NE steps: 0, 1, 4, 9, 16, 25, ...The last line will be referred to as the white list.
1 NE step: 1, 3, 7, 13, 21, 31, ...
2 NE steps: 3, 4, 7, 12, 19, 28, ...
3 NE steps: 7, 9, 13, 19, 27, ...
4 NE steps: 12, 13, 16, 21, 28, ...
union: 0, 1, 3, 4, 7, 9, 12, 13, 16, ...
Note that all of the squared lengths are integers. These are the allowed squared lengths of the "hypertenuse" block that preserves the distance between the two hinges. Now, the two hinges are connected to the square, so their coordinates have to differ by an integer combination of the vectors t,u,v,w mentioned previously.
Let's redo an exercise we did in a different basis. A general integral combination of the vectors t,u,v,w - the vector difference between the two hinges, as calculated from the block containing the square
At + Bu + Cv + Dwhas the squared length equal to
A2 + B2 + C2 + D2 +There are no AC and BD terms because the pairs t,v and u,w are orthogonal: even in the upper part of the text, I have switched the sign of "1/2" in w to "-1/2", apologies to old readers. ;-)
+ AB - CD + sqrt(3) (AD + BC)
Now, because the squared distances that can be supported by the "hypertenuse" blocks are integers, it follows that AD+BC has to vanish. Consequently, it can't be true that exactly three of the numbers A,B,C,D are nonzero: either 4 or 2 (or fewer) are nonzero. If 2 (or fewer) numbers among A,B,C,D are nonzero, we have either B=D=0 or A=C=0, which returns us to the Pythagorean numerology and 3-4-5 is the smallest solution (optimization of the 3-4-5 triangle may be discussed separately) , or A=B=0 or C=D=0 which are not allowed because the construction would only be attached to one of the sides of the square.
If all A,B,C,D are nonzero, which is the only room for solutions that may differ from the Pythagorean 3-4-5 concept, we have to check the combinations
A,B,C,D = K,L,K,-Land their equivalents with sign flips and permutations that don't change the essential geometry (and the new angles at the special hinges). The apperance of K,L = 3,3 or more or K,L = 2,4 or more would already produce the total squared length above 31. We must also check
A,B,C,D = K,K,L,-L
K,L = 1,1 or 1,2 or 2,2 or 2,3
A,B,C,D = 1,2,2,-4.However, it produces the squared length of 1+4+4+16+2+8 = 35 or 1+4+4+16-2-8 = 15 (for -1,2,2,4) which are not on the "white list" and are getting too high, anyway. Similar small values of A,B,C,D that are not pairwise equal may be seen to produce too big a squared length, or a squared length that is not in the allowed list. For example, for A,B,C,D=1,2,3,-6, one gets AD+BC=0. However, the squared length is 1+4+9+36+-(2+18)=50+-20 which is 30 or 70, too large.
That's why we have reduced the unknown yet promising solutions to the cases when all A,B,C,D are nonzero and expressed in terms of K,L as above. In the two inequivalent cases that make AD+BC vanish, namely K,L,K,-L and K,K,L,-L, the squared length of the vector (the sum of squares of A,B,C,D plus AB-CD) is equal to 2K^2+2L^2+-2KL or (3K^2+3K^2 or K^2+L^2).
The result must belong to the allowed list of squared lengths, 0, 1, 3, 4, 7, 9, 12, 13, 16, ... Clearly, the length 1 would only produce constructions with angles divisible by 30 degrees again which is no good, as proved at the beginning. Let's continue with the white list.
What about the squared length equal to 3, 7, 9, or 12?
The odd numbers can't be obtained as 2K^2+2L^2+-2KL because the latter is even. They can be written as K^2+L^2 or 3(K^2+L^2) but only if one of K,L vanishes... We want both K,L nonzero, as mentioned previously (because the construction would only be attached to one side of the square).
The smallest number of the form K^2+L^2 for positive integers K,L that is on the white list is 13 for K,L=2,3 or 3,2: numbers 2,5,8 are not on the white list. And 18 = 3^2+3^2 that would be just a little bit bigger is not on the white list, either.
The template 3(K^2+L^2) is clearly even less useful to create small solutions. The smallest allowed values of this tripled sum for positive integers K,L, namely 6,15,24..., are not on the white list, either. So far, K^2+L^2=9+4=13 is the only nontrivial small solution we found.
Finally, we must deal with the template 2(K^2+L^2+-KL); of course, the negative sign is better to produce smaller results. This can only match the even numbers on the white list, namely 4,12,16..., because it is even. K^2+L^2+-KL would have to be equal to 2,6,8... However, 2,6,8 can't be written in this form: 2,6 are equal to 2 modulo 4, but K^2+L^2+-KL can't be 2 mod 4. And 8 is also impossible for similar reasons.
So the only new small solution we found was one based on the hinges whose distance is sqrt(13).
Top intersecting solution
The assumption of just 2 vertices (hinges) that are not combinations of t,u,v,w is severely violated in the state-of-the-art best solutions. At the top, there is bbzippo's non-intersecting solution with 23 extra linkages.
Frictionless intersecting solutions can go down to incredible 15 extra linkages. This one is an example - a modified JollyJoker's structure:
Note that the original square with the pink vertices is rotated by 45 degrees. There are 3 additional - blue - vertices in the picture. Their 6 coordinates are constrained by 7 conditions on the length; this overdetermined system of conditions (by one) is just the right amount to fix the angle of the square with pink vertices.
The 7 distances that are fixed include the 3 vertical length-one distances from the adjacent pink vertices of the square; 2 length-one distances of the central light blue new point from the two dark blue new points on the sides; and 2 length-sqrt(3) distances of the upper blue points from the most distant pink vertices on the opposite side - that are realized by the di-triangle rhombuses.
This new solution brings you into an entirely new class of possibilities. Just add N vertices to the plane - outside the integer combinations of t,u,v,w - such that 2N+1 distances between these vertices (either between pairs of them, or between the vertices and arbitrary points in the "lattice" of integer combinations of t,u,v,w) belong to the white list (i.e. can be realized by inserting parts of triangular trusses).
Such a new template looks very general and it would be very time-consuming to look for all solutions, even pretty small ones, but I can still argue that even this general class actually doesn't exhaust all the possibilities. One could also "add the angles" etc.
Subscribe to:
Posts (Atom)
