iPad 2: even larger?

Serious update: See live coverage of the iPad 2 event.

In 2010, Apple took an iPod Touch and - bchřšžprd - made it bigger. This iPad became an important companion of Gene's - and of others. Tomorrow, Apple is likely to release iPad 2.

They took an iPad - bchřšžprd - and made it bigger. :-)



As you can see, it has become very convenient.

They will also give you about 30 square meters of sensitive glass so that you may improve your apartment and your street.




The glassy system has been tried in a family of beta testers - an ordinary working family in Libya:



That was before the civil war - that became the topic of the 4883rd episode of the Star Wars:



More seriously, this is how the shape of iPad 2 could look like:



And iPhone 5 is likely to have an edge-to-edge display:

Global warming panic explained

One of those computer-narrated, animated dialogues. But this one is really funny and realistic:



My favorite line was "That was in the old times. Now progress is achieved by scientists falling in line and keeping their doubts to themselves." :-)

The same user has created similar excellent videos on raising of the taxes, affirmative action, feminism, and others.

Thanks to Marc Morano

The big book of brain games: a puzzle

Ultimate spoiler:



A record solution that TRF reader bbzippo found a few years ago: 23 extra linkages, no intersections. Only previous record holders are discussed in detail here:

This solution of mine uses 31 extra edges or, if you allowed frictionless intersections and if you could shorten the lower left detour by one small triangle, it would use 29 extra edges. Go to the end of the article for comments why this is a valid solution.

---

Phil Gibbs' blog that I regularly read and learn from - and that actually doesn't irritate me in any way - posted a very cool Christmas puzzle from “The Big Book of Brain Games” by Ivan Moscovich. Most of the puzzles are claimed to be easy but puzzle number 331 is subtle and very interesting:

Draw a square consisting of four equally long connecting line segments hinged at the vertices. Such a structure may degenerate into a rhombus if you apply some pressure. How many additional interlinks of the same length must be supplemented to prohibit this excessive degree of freedom and to prevent the square from being tilted? The interlinks must belong to the same plane as the quad and each one may only be pegged to others at the endpoints.

So far, I can't link to the original blog now because you would find a solution. The owner of the blog and his fastest reader found a solution with 43 extra linkages. After I was told what it was, your humble correspondent found a generalized solution of the same kind that only uses 29 extra linkages, if you allow me to draw frictionless intersections, or 31 extra linkages, if you don't.




I recommend you to waste a few hours with drawing pictures whose faces have internal angles that are multiples of 30 degrees. It's useful because you will learn that one can waste a lot of time by drawing seemingly attractive structures if he or she makes a completely wrong assumption or too constraining an Ansatz about the solution. ;-)



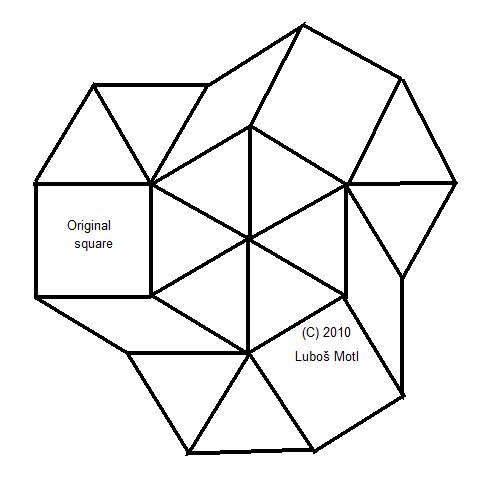An example of a solution attempt that doesn't work. Your humble correspondent drew many of them! :-)

It seems pretty clear to me that no solution of the kind that is describe in the previous big paragraph can exist. You must make the structure solid by thinking outside the box a little bit. :-) If it helps you, here is a Mathematica 7 code that allowed me to find my more nontrivial solution once I understood the broader concept that is actually promising:

finds = {{0, 0, 0, 0, 0, 0, 0}};

(* next, separated line with input *)
Dynamic[{a, b, lenVsq, c, d, e, f}]
Dynamic[MatrixForm[finds]]

(* next, separated line with input *)
For[a = 1, a <= 7, a++,
For[b = -7, b <= 7, b++,

v = {a, 0} + b*{1/2, Sqrt[3]/2};
lenVsq = v[[1]]*v[[1]] + v[[2]]*v[[2]];

For[c = -5, c <= 5, c++,
For[d = -5, d <= 5, d++,
For[e = -5, e <= 5, e++,
For[f = -5, f <= 5, f++,

u = {d/2 + c, d*Sqrt[3]/2}
- {f*Sqrt[3]/2, f/2 + e};

lenUsq = u[[1]]*u[[1]] + u[[2]]*u[[2]];

finds =
If[(c*c + d*d)*(e*e + f*f) != 0 &&
Abs[lenUsq - lenVsq] < 0.00001,
finds~Join~{{a, b, lenVsq,
c, d, e, f}}, finds];

]
]
]
]
]
]

I guess that if you're not told the main idea, chances are that even the code above will be useless for you. Their "solution 43" as well as my "solution 29/31" have already been posted to the web but I won't give you coordinates before some of you try to solve it - and perhaps find an even more economical solution?

Bonus: a no-go theorem

I am sure that I was not the only one who got stuck for some time with tests of pictures like this one:

Well, JollyJoker is another victim because the picture above was offered by him.

Note that there is a whole class of pictures where all the linkages are either vertical, or horizontal, or have another azimuthal angle that is a multiple of 30 degrees. Correspondingly, all internal angles of all faces are multiples of 30 degrees as well - 30, 60, 90, 120, or 150 degrees.

With some help from TRF, it's straightforward to prove that no picture of this kind can be rigid.

First, use (0,0), (1,0), (0,1), (1,1) for the vertices of the square. If all edges have one of the allowed azimuthal angles mentioned above - 0, 30, 60, 90, 120, or 150 degrees (or the opposite-direction edges whose azimuthal angle differs by 180 degrees), then all vertices or hinges indirectly connected to the square have coordinates that are integer linear combinations of the following four vectors:

t = (1, 0)
u = (1/2, sqrt(3)/2)
v = (0, 1)
w = (sqrt(3)/2, -1/2)

Note that the nontrivial numbers are, up to the last sign, sines and cosines of 30 or 60 degrees. However, if you have a collection of points whose coordinates are

at + bu + cv + dw,
a, b, c, d are integers,

then you can see that both coordinates of the points are integer combinations of 1/2 and sqrt(3)/2. However, you may deform the picture by preserving vectors t,u and rotating v,w into v',w':

v' = (sin(phi), cos(phi))
w' = (sin(120°+phi), cos(120°+phi))

---

point' = at + bu + cv' + dw',
a, b, c, d are integers.

All edges whose length was equal to 1 in the old diagram - composed of points with coordinates point - have to have the length 1 in the new diagram composed of points with coordinates point'. That's because

t, u, t-u; -t, -u, -t+u;
v, w, v+w; -v, -w, -v-w

are the only integer combinations of vectors t,u,v,w whose length is (or was) exactly equal to one (see below). However, if you replace v,w by v',w' in the expressions above, it's still true that all the vectors will have length equal to one. That proves that the diagram may be tilted.

To show my lemma, recall that the general linear combinations of the vectors t,u,v,w may be written as

{ (A+B sqrt(3))/2, (C+D sqrt(3))/2 }

Four times the squared length of this vector should be equal to 4 but it is

+ A² + 3B² +
+ C² + 3D² +
2 sqrt(3) (AB+CD)

where A,B,C,D are integers. This can only be equal to 4 if (AB+CD) vanishes - it's the coefficient of the square root of three, an irrational number that can't cancel against others because of the integrality of the coefficients. Moreover, the four positive terms on the first two lines have to add up to four.

It may only happen if this number four arises as 4+0+0+0 or 0+0+4+0 or 1+0+0+3 or 0+3+1+0 - all higher numbers are easily seen to exceed 4. Moreover, 1+3+0+0 and 0+0+1+3 are also forbidden because AB+CD would be nonzero (plus minus three). That proves that there are only 6 possible vectors and their 6 opposite vectors whose length is equal to one. In terms of the old basis, they were written as

t, u, t-u; -t, -u, -t+u;
v, w, v+w; -v, -w, -v-w

You see that the combinations of t,u are decoupled from the combinations of v,w, so you may rotate v,w separately from t,u (that you may keep fixed, for example), and it won't break any of the linkages because all linkages that existed will continue to have length equal to one.

This no-go theorem is an example of the fact that you may get stuck in drawing seemingly pretty pictures and you may hope that if you combine the flowers in a cleverer way than an hour ago, you will succeed. However, it can be shown that the whole infinite class of such pictures is ruled out.

The same thing holds in many other contexts. In particular, all people working on discrete theories of spacetime - or any quantum theory of gravity that is not equivalent to string theory - may spend lots of time (it's decades or centuries rather than hours in this case) by fabricating more convoluted models.

But it can be seen that there are no consistent non-stringy theories of quantum gravity. The latter statement and its proof are more complex than the example above - and the proof arguably demands a lot of knowledge from the readers - but the statement is equally true as the no-go theorem for solutions to the linkage problem whose angles are multiples of 30°.

You need to add a new player - internal angles that are not multiples of 30 degrees, in this case - to have a chance to find a solution. Then you enter a broader, different set of candidates - the counterpart of the string theory landscape - and in this set of candidates, which encourages you to study different issues than in the wrong class and to generalize them in different ways than before, you may actually construct correct and/or minimal solutions to your problem.

---

Spoilers: best solutions with 31 extra edges

The best solution available at this moment was found by your humble correspondenent by refining the Pythagorean idea. The Pythagorean solution was independently found by Phil Gibbs, Bill K, and Honza U. who was the first successful TRF reader to solve the challenge:



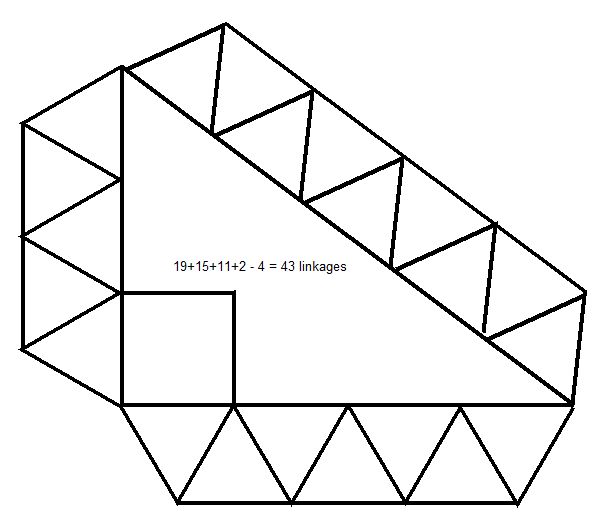
The solution uses the Pythagorean identity 3^2+4^2=5^2. The three "rigid bridge elements" contain 19, 15, 11 linkages, respectively, and 19+15+11+2-4 = 43 new linkages. The number doesn't change if you allow self-intersections (a point that was misinterpreted by Honza).

Mr/Ms Imho cannot be counted as a successful solver because he or she thought that you can erase the whole bridge elements and preserve just the 3+4+5 thin linkages surrounding the large 3-4-5 Pythagorean triangle (which would mean 12-2=10 extra linkages). Well, indeed, such a construction wouldn't be rigid at all and I hope that Mr/Ms Imho is not a professional architect. :-)

However, using the Mathematica code above, I found a more efficient solution that only uses 31 extra line segments:



or, if you allow frictionless intersections of the line segments, 29 extra linkages:



It is similar to the 3-4-5 Pythagorean triangle except that the catheti are not 3 and 4 but rather 2 and 3. You may complain that the hypotenuse is not an integer. Indeed, it's not: its length is sqrt(2^2+3^2) = sqrt(13).

However, one can create a rigid line segment of length sqrt(13) using the equilateral triangular truss, too. Draw a triangular truss that includes horizontal lines and the point (0,0). Make three steps to the East (right): the coordinate of the final point will be (3,0).

Now, make a step to the (almost) Northeast. You will add (1/2, sqrt(3)/2) to the coordinates of your point so the final point will be

(3.5, sqrt(3)/2)

The squared length of this vector - the distance between the two points of the triangular truss - equals

3.5² + 3/4 = 12.25 + 0.75 = 13

just like previously. So three pieces of the triangular bridge construction may be connected just like in the case of the 3-4-5 Pythagorean triangle and the right angle of the square is ensured in this way.

The Mathematica program above, which has only searched through a set of sufficiently "small" solutions, has also found a solution with the hypotenuse equal to sqrt(39). In that solution, one has to use both directions of the triangular trusses on all three sides of the big triangle.

---

Exhaustive search: a proof of minimality

It's actually not hard to find the 29/31 solution above in a controlled, exhaustive search for economical solutions. Earlier in this text, I showed that there must exist internal angles that are not multiples of 30 degrees. Obviously, there must exist at least two such hinges where the internal angles not divisible by 30 degrees exist.

At least two such hinges are indirectly connected to the square by some linkages. Look at these two hinges. Of course, in the minimum setup, there will be exactly two such linkages.

The assumption in the previous sentence was proved to be wrong. The current most economical solution known to me - at the top of the article - depends on four hinges whose internal angles differ from multiples of 30 degrees. This fact invalidates the rest of the proof but it may still be interesting for you to read it.

To fix the angles of the square, the distance between these two linkages must be protected by an additional network of linkages - which will become the "hypertenuse" in the Pythagorean-based solutions. It's almost guaranteed that the minimal structure that preserves the distance is made out of a triangular truss.

Now, you may enumerate all the squared distances you may obtain from a triangular network. If you classify them by the number of "Northeast" steps, the allowed squared distances are:

0 NE steps: 0, 1, 4, 9, 16, 25, ...
1 NE step: 1, 3, 7, 13, 21, 31, ...
2 NE steps: 3, 4, 7, 12, 19, 28, ...
3 NE steps: 7, 9, 13, 19, 27, ...
4 NE steps: 12, 13, 16, 21, 28, ...

---

union: 0, 1, 3, 4, 7, 9, 12, 13, 16, ...

The last line will be referred to as the white list.

Note that all of the squared lengths are integers. These are the allowed squared lengths of the "hypertenuse" block that preserves the distance between the two hinges. Now, the two hinges are connected to the square, so their coordinates have to differ by an integer combination of the vectors t,u,v,w mentioned previously.

Let's redo an exercise we did in a different basis. A general integral combination of the vectors t,u,v,w - the vector difference between the two hinges, as calculated from the block containing the square

At + Bu + Cv + Dw

has the squared length equal to

A² + B² + C² + D² +
+ AB - CD + sqrt(3) (AD + BC)

There are no AC and BD terms because the pairs t,v and u,w are orthogonal: even in the upper part of the text, I have switched the sign of "1/2" in w to "-1/2", apologies to old readers. ;-)

Now, because the squared distances that can be supported by the "hypertenuse" blocks are integers, it follows that AD+BC has to vanish. Consequently, it can't be true that exactly three of the numbers A,B,C,D are nonzero: either 4 or 2 (or fewer) are nonzero. If 2 (or fewer) numbers among A,B,C,D are nonzero, we have either B=D=0 or A=C=0, which returns us to the Pythagorean numerology and 3-4-5 is the smallest solution (optimization of the 3-4-5 triangle may be discussed separately) , or A=B=0 or C=D=0 which are not allowed because the construction would only be attached to one of the sides of the square.

If all A,B,C,D are nonzero, which is the only room for solutions that may differ from the Pythagorean 3-4-5 concept, we have to check the combinations

A,B,C,D = K,L,K,-L
A,B,C,D = K,K,L,-L
K,L = 1,1 or 1,2 or 2,2 or 2,3

and their equivalents with sign flips and permutations that don't change the essential geometry (and the new angles at the special hinges). The apperance of K,L = 3,3 or more or K,L = 2,4 or more would already produce the total squared length above 31. We must also check

A,B,C,D = 1,2,2,-4.

However, it produces the squared length of 1+4+4+16+2+8 = 35 or 1+4+4+16-2-8 = 15 (for -1,2,2,4) which are not on the "white list" and are getting too high, anyway. Similar small values of A,B,C,D that are not pairwise equal may be seen to produce too big a squared length, or a squared length that is not in the allowed list. For example, for A,B,C,D=1,2,3,-6, one gets AD+BC=0. However, the squared length is 1+4+9+36+-(2+18)=50+-20 which is 30 or 70, too large.

That's why we have reduced the unknown yet promising solutions to the cases when all A,B,C,D are nonzero and expressed in terms of K,L as above. In the two inequivalent cases that make AD+BC vanish, namely K,L,K,-L and K,K,L,-L, the squared length of the vector (the sum of squares of A,B,C,D plus AB-CD) is equal to 2K^2+2L^2+-2KL or (3K^2+3K^2 or K^2+L^2).

The result must belong to the allowed list of squared lengths, 0, 1, 3, 4, 7, 9, 12, 13, 16, ... Clearly, the length 1 would only produce constructions with angles divisible by 30 degrees again which is no good, as proved at the beginning. Let's continue with the white list.

What about the squared length equal to 3, 7, 9, or 12?

The odd numbers can't be obtained as 2K^2+2L^2+-2KL because the latter is even. They can be written as K^2+L^2 or 3(K^2+L^2) but only if one of K,L vanishes... We want both K,L nonzero, as mentioned previously (because the construction would only be attached to one side of the square).

The smallest number of the form K^2+L^2 for positive integers K,L that is on the white list is 13 for K,L=2,3 or 3,2: numbers 2,5,8 are not on the white list. And 18 = 3^2+3^2 that would be just a little bit bigger is not on the white list, either.

The template 3(K^2+L^2) is clearly even less useful to create small solutions. The smallest allowed values of this tripled sum for positive integers K,L, namely 6,15,24..., are not on the white list, either. So far, K^2+L^2=9+4=13 is the only nontrivial small solution we found.

Finally, we must deal with the template 2(K^2+L^2+-KL); of course, the negative sign is better to produce smaller results. This can only match the even numbers on the white list, namely 4,12,16..., because it is even. K^2+L^2+-KL would have to be equal to 2,6,8... However, 2,6,8 can't be written in this form: 2,6 are equal to 2 modulo 4, but K^2+L^2+-KL can't be 2 mod 4. And 8 is also impossible for similar reasons.

So the only new small solution we found was one based on the hinges whose distance is sqrt(13).

Top intersecting solution

The assumption of just 2 vertices (hinges) that are not combinations of t,u,v,w is severely violated in the state-of-the-art best solutions. At the top, there is bbzippo's non-intersecting solution with 23 extra linkages.

Frictionless intersecting solutions can go down to incredible 15 extra linkages. This one is an example - a modified JollyJoker's structure:



Note that the original square with the pink vertices is rotated by 45 degrees. There are 3 additional - blue - vertices in the picture. Their 6 coordinates are constrained by 7 conditions on the length; this overdetermined system of conditions (by one) is just the right amount to fix the angle of the square with pink vertices.

The 7 distances that are fixed include the 3 vertical length-one distances from the adjacent pink vertices of the square; 2 length-one distances of the central light blue new point from the two dark blue new points on the sides; and 2 length-sqrt(3) distances of the upper blue points from the most distant pink vertices on the opposite side - that are realized by the di-triangle rhombuses.

This new solution brings you into an entirely new class of possibilities. Just add N vertices to the plane - outside the integer combinations of t,u,v,w - such that 2N+1 distances between these vertices (either between pairs of them, or between the vertices and arbitrary points in the "lattice" of integer combinations of t,u,v,w) belong to the white list (i.e. can be realized by inserting parts of triangular trusses).

Such a new template looks very general and it would be very time-consuming to look for all solutions, even pretty small ones, but I can still argue that even this general class actually doesn't exhaust all the possibilities. One could also "add the angles" etc.

Percentage of girls: a puzzle

Try to solve this puzzle:



Steve Landsburg gives a wrong answer, different from 50%, while CommunistStalinistSwine gives a correct one, 50%.




The chance that a birth produces a girl remains 50% regardless of the laws. So unless some children are deliberately aborted or otherwise killed, the proportion of girls remains 50%.

Another question is the percentage of girls in a family with child(ren) averaged over all families with child(ren). As CommunistStalinistSwine correctly writes, the answer is

(0/1) * 1/2 + (1/2) * 1/4 + (2/3) * 1/8 + ... =
= 1 - ln(2) =
= 0.30685...

Your humble correspondent kindly added the analytic and numerical result for the sum. Have you ever encountered the Taylor expansion for "ln(1-x)"? And substituted "x=1/2" into it haha?

Note that the two results, 31% and 50%, differ. It's because each rare family with many daughters raises the family average just a little bit - because it is just one family - but it raises the proportion of girls in the society a lot - because it offers many girls.

This discrepancy is actually an example of the inability of the anthropic principle to produce quantitative predictions of any probabilities.

Imagine that the families above are Universes in a multiverse. You want to calculate the odds of being female. If you take an average Universe and an average observer in it, you obtain 31%. If you take an average observer in the whole multiverse, you obtain 50%.

It matters whether you insert additional "average something" layers into your calculation or not. In reality, such extra layers don't change the result from 31% to 50%. They may change the odds by dozens of orders of magnitude or more.

If you look for a "typical cell" of an organism, it is much more likely to be a cell of a big organism - such as a polar bear that are not endangered, just threatened - than a small one. So looking for a typical cell on the Earth ends up with a very different result than looking for a typical cell in a typical organism - which is a bacterium. The former is much more likely to be a cell of a large organism.

By the way, while solving his puzzle, Landsburg mentioned a family that has 12 boys. The parents should be arrested because according to the very laws mentioned above, the last 11 boys were born and maybe even conceived illegally.

A loophole

There is actually a subtle assumption in CIP's formula that has led to the result 31%: we only considered families that already have a son, and that have already finished their childmaking.

If we had included families that haven't had a son yet, the percentage of girls in a family averaged over families with at least 1 kid would increase and arguably stay at 50%. To calculate the percentage by a sum, however, we would have to know at least the relative proportion of 1-girl and 2-girl families at every moment. This percentage, reflecting the typical fertility of a family - in a similar way as in a society without the 1-son constraint - wasn't determined in the formulation of the problem.

Because of this loophole, you may explain the lower result of 31% obtained previously as an artifact of the selection bias - that we have only considered the "completed families" that have already received their son. This selection bias has increased the percentage of boys and decreased the percentage of girls. Without this selection bias, the average percentage of girls has to remain at 50% even in an average family under-or-after construction.

Google

Later, I learned that this problem was asked during interviews at Google. The official answer is 50:50, thank God.

Shoveling snow may be fun

We have lots and lots of snow in Central Europe.



Meanwhile, as Roy Spencer reports from the very place, Cancún in Mexico experiences the Gore Effect. They are living through the coldest December 7th on record.




Two weeks ago, Al Gore admitted that his support for the ethanol biofuels was a mistake that has raised food prices, among other things. Sorry, folks, I was wrong and you had to pay tens or hundreds of billions.

So far, Gore won't tell us that his whole life was a gigantic mistake that has cost us hundreds of billions of dollars and could cost us trillions or tens of trillions of dollars if we didn't stop the jerk. He's not brave enough to admit that much. Al Gore should have been responsible for his deeds from his very birth - because this was already pretty much his biggest sin. :-)

One of Al Gore's climate groups shrinks. I guess it won't impact himself.

---

News from the Google company



Google has presented the Cr-48 laptop with the Chrome OS, based on the Chrome browser. Note that Cr is the chemical formula of chromium.

Also, Google has opened the Google Webstore which is their database of "web applications" or bookmarks or extensions - possibly paid ones - created for Google Chrome in such a way that it should resemble the Apple AppStore as much as possible. ;-)

Slippery Lube

This is not a real blog entry, just a page posted on December 30th, 2010, as a reply to Steve Landsburg on his blog. His entry is called "Slippery Lube". The title is very funny but that's where the quality of the article ends.

He is trying to defend a wrong solution to a simple problem about the proportion of girls in a country where the son has to be the last child in each family.

My comment is below (it's just for me and the people who Google search for "Slippery Lube") - and obviously, he is not approving comments that disagree with him:

---

Dear Steve,

honestly, I really don’t enjoy neverending debates and arguments about trivial issues which is why I de facto closed the thread and I surely don’t plan another blog entry about this trivial puzzle. The issue is totally clear. It’s clear that every long enough sequence of births will produce exactly 50% of girls and 50% of boys, regardless of the parents’ superstitions and their algorithms to stop reproduction at various points.




The average non-weighted proportion of girls in a family is a subtle exercise, and it’s nice that you also calculated it’s 30.6% (Taylor expansion for a 1-ln(2)), which is strictly below 50% because the small one-boy-only families are overrepresented in computing the average, but it’s not the same thing as the fraction in the society that is exactly 50% for any sustainable society or country or nation. To get the latter, one has to weight the families by their numbers in computing the average proportion, and one always gets 50% exactly in this way as long as the nation is sustainable.

The only way to get a number different from 50% is to replace the nation by a limited history that goes extinct after their families hit the wall – by having the first son. This limited suicidal sect simply can’t be called a nation or a country.

Even if you take these limited histories, the properly weighted average of the proportion of girls over such histories will still be 50%. All qualitative arguments that the number is different from 50% have errors in it. For example, if one also counts incomplete families, he could say that large families have a higher fraction of girls while the 1-child families are balanced, so the boys will never catch up. This is a wrong statement because if the couples would normally have many children, the stopping rule creates some highly-female families, but the same stopping rule also increases the proportion of families who have 1 boy and no girls – the pairs angry about the government because they wanted to have many kids but the government stopped them after the 1st kid. This demographics doesn’t exist for 1-girl-only families which means that 1-boy-only families prevail over 1-girl-only families. The full calculation, of course, implies that the two effects are balanced and the fraction is exactly 50%-50%.

All such questions may be answered within minutes. I really don’t understand the point of spending days on this trivial issue. Please, if you think that 50% is a wrong answer, contact Google that had 50%-50% as the official right answer to this puzzle during their hiring process. Complain over there. I didn’t use this simple math problem to dismiss candidates for jobs in my company even though I fully understand why Google did. It’s a very good task to find and throw away the people who will get distracted from common sense and from simple, fundamental math arguments by noise and who will immediately start to think about complicated yet irrelevant technicalities – which is exactly what you did which is why you couldn’t work at Google but you instead work in the Academia that often supports this contrived way of thinking that is detached from the reality and everything important in it. In Google, these people would only contribute inpenetrable and hard-to-find bugs to the software. They lack the clarity of their thinking which is surely important in the commercial sector but I think it should be required in the scholarly work, too.

The “worth the effort to ignore LM” probably came from John Baez. He began to ignore me – as well as all people whose remarks actually make any sense – which is why he ended up as a mentally ill person who believes that he is the new Messiah who will save the Earth somewhere in Singapur. Feel free to follow him. Everyone who deliberately starts to ignore rational arguments will inevitably end up in the hell of irrationality.

Best wishes
Luboš

Climate Change Prognosticator: a new omniscient climate model

WHN covers the Climate Change Prognosticator, featuring a tour of the Brick Moon Meteorological Laboratory.




Bonus points for spotting an anagram, a couple of allusions to H. P. Lovecraft and to the Wizard of Oz, and an obscure architecture pun.

There is a video of the actual CCP automaton on my YouTube channel.

Via klimaskeptik.cz

Red Redemption: Fate of the world

In 2006, Red Redemption, openly supported by Oxford, BBC, and the Environmental Change Institute, released a Flash game called Climate Challenge.



Click to zoom in.

In the game, you were a "European president" who had to suppress the whole European population as Hitler and Stalin combined with the goal of reducing the CO2 emissions, screwing the people, bribe politicians from other continents, and keeping yourself in power (play now the monstrosity directly at the BBC website).

Of course, these folks haven't been arrested so they continued to "work". At the end of October 2010, they will release a game that is more ambitious,

Fate Of The World (game website, trailer)

In the new game, you are no longer just a European dictator which was way too modest a job.



Now you are chosen the global dictator - the head of the G.E.O. junta - who is hired immediately when the 2010 climate talks fail (see the trailer) and whose task is do everything to reduce the emissions of CO2 in the world. Here are some of your basic options; they became much more "juicy" relatively to the bureaucratic elimination of power plants etc. in the 2006 game:



Click to zoom in.

On each continent, you can introduce "mandatory euthanasia" for $100 billion - a policy to kill all the old and ill people. Or you can pay the same money to develop special bio-weapons to predictably exterminate whole nations. For the same payment, you may also induce a regime change just to overthrow politicians who are climate skeptics or who are otherwise hostile to your world government and replace them with "biddable", corrupt politicians of your choice.

So this is what they plan if the 2010 climate talks will fail, and be sure that they will? Even if the creators of the game don't intend it, it's clear that some groups will worship the game as a computer model whose lessons justify "action". After all, the likes of the IPCC are already taking much less realistic computer games seriously today.




Let me admit that I really think that the people who will be earning money by promoting these recipes for the future should be quickly and preemptively arrested if not executed for planned crimes against humanity. This topic is no material for jokes in a world where you can find actual unhinged lunatics, and some of them are very powerful (e.g. the U.S. "Science Czar", Mr Holdren), who indeed want to introduce inhuman and anti-market measures in order to "regulate carbon dioxide".

You may say: this is just a game. You don't want to arrest or execute someone who just wrote a video game, do you? Well, Mein Kampf was also "just a book". For a while, before it became clear that it wasn't just a book: it was a detailed plan to bring a decade of genocide (originally planned as a millennium) to the whole European continent - and beyond. As long as there exists a credible threat that some people will try to actually realize these insane things with carbon regulation in the future, we should better view games and books with details about such a hypothetical future to be parts of the planning process for the genocide, and the courts should deal with the perpetrators accordingly. You may call it the precautionary principle.

By the way, if you're worried that mandatory euthanasia, bioweapons to exterminate continents, or liquidation of democratic politicians are your only options in the game, you shouldn't worry so much.

You may also initiate a global nuclear war. This climatic option also reflects a reality: Rutgers professor Alan Robock just explained his friend and comrade Fidel Castro what are the climatic impacts of a nuclear war. Sweet.

On a positive note, there are a few positive decisions you may do in the game, too. For example, you may "sponsor denial lobby" - but only $50 billion, instead of $100 billion for the recommended "projects" above. And you may also build nuclear power plants - but you will become hated if you do so. As you can see, genocide is the only option you can take.

Holy cow.

Don't expect the punishment for the disgusting jerks anytime soon. In August 2010, Nature published a positive review about this game promoting several methods of global genocide. It's a "platform for learning about science" and "serious fun," we learn.

Huh!? What is so scientific about clicking at a button to kill millions or billions of people? People used to be good at these things long before they began to study science. Maybe they were not as good in genocide as climate alarmists, but it's still true that there is absolutely no science in genocide or in the global warming fearmongering.

See also: The 10:10 movement plans to exterminate skeptical kids and adults

Hat tip: Willie Soon

---

Update: The Telegraph

The Telegraph joined those who promote the new game. According to the conservative newspapers, it's an "interesting idea" to solve the climate crisis by designing a virus that kills millions.

Many brutal adjectives seem more appropriate than "interesting" to me.

One son on Tuesday: a probabilistic puzzle

John Baez, a savior of the Earth, discusses an interesting puzzle that was sent to him by Greg Egan:

A few months ago I read about a very simple but fun probability puzzle. Someone tells you:

“I have two children. At least one is a boy born on a Tuesday. [And if it were not the case, I would have told you.] What is the probability I have two boys?”

Try to solve it yourself. John Baez mentions that you would think or he would think that the information about Tuesday is irrelevant because the days of the week are independent of the sex and we only care about the latter.

So you would think that there are 4 equally represented groups of 2-kid families, namely boy-boy, boy-girl, girl-boy, and girl-girl families where the two hyphenated words refer to the younger and older kid, respectively. Only the girl-girl families are eliminated, and 1 of the remaining 3 groups is a two-boy family, so the conditional probability is 1/3.

However, that's a wrong result. The information about the Tuesday actually does matter. Here's why:

Correct solution

In all families with exactly 2 children, one may label the children as the "younger" and "older" one, even if the difference is just in seconds.

Each kid may be born on any day and have any sex, so there are 14 equally likely possibilities for each child. The two children are independent (forget that the phenomenon of twins tends to increase the same-day pairs), so there are 14 x 14 possibilities for two kids. Each of these 14 x 14 possibilities is equally likely. So 1/196 of the world's families with exactly 2 kids fits each condition.




Among the 196 types of the families, how many of them contain at least one Tuesday son? Well, in 14 of them, the younger kid is a Tuesday son (the older one may be anything chosen from the 14 possibilities). In 14 other of them (the younger can be anything), the older one is a Tuesday son. However, I have counted the families with two Tuesday sons twice. So there are 14+14-1 = 27 possibilities among the 196 for which the condition "at least one kid is a Tuesday son" is satisfied.

This is the assumption which is a part of the calculation of the conditional probability. We need the other part, too. Among these 27/196 of the families, 13/196 of all families have two boys, by pure counting, so the result is

P = 13/27

as the fraction of the families that satisfied the condition. Note that it is just slightly less than 1/2 = 13.5/27 i.e. much more than 1/3. I had to highlight the result because almost no one reads the full article and almost no one notices that the right results is neither 1/3 nor 1/2.

Indeed, the large difference of the right result from 1/3 appears because one de facto identifies one of the sons by mentioning that it is the kid from Tuesday. If you assumed there were infinitely many days in a week and you would take any family with at least one Tuesday kid, the "Tuesday" information would identify this kid completely (two Tuesday kids would be infinitesimally unlikely), and the question what is the probability of 2 sons would be reduced to the question what is the probability that the other, equally specific kid - the non-Tuesday kid - is male - which is of course 1/2.

I will discuss this "identification" and reasons why the result is close to 1/2 at the very end.

Indistinguishable kids' bound states

With kids that would satisfy the Bose or Fermi statistics, the counting would be different but equally straightforward. Instead of 14 x 14 = 196 possibilities, one has 14 x 15 / 2 = 105 for bosons (the symmetric triangle) and 14 x 13 / 2 = 91 (the antisymmetric triangle) for fermions. Among the 105 or 91 options, how many of them contain at least one Tuesday son? Well, in these two cases, we can't say which of them is older and younger: they're identical.

So if there is at least 1 Tuesday son, the number of states with at least 1 Tuesday son is 14 for the bosons - we can just create the other particle into the 1-particle state - or 13 for the fermions - we can also add the second creation operator, but with another Tuesday son, the state will vanish because of Pauli's exclusion principle.

Among these 14 or 13 states respectively, for bosons and fermions, 7 or 6 are two-son states, respectively. So the odds are 7/14 = 1/2 for the bosons and 6/13 for the fermions. Note that the bosons literally saturate the 1/2 bound while the fermions are just slightly below it.

Why not one third?

Finally, I want to comment on "why the information about Tuesday matters". If we sum up the probabilities for the problems where the son is born on Sunday, Monday... and up to Saturday, shouldn't we get the same result? And by symmetry, the result must be equal for all 7 days, so doesn't each term have to be 1/3?

The answer is that we can't add the probabilities in this way because the "at least one Monday son" etc. are assumptions, not propositions conditioned by these assumptions, and they're not disjoint. At any rate, the calculation is nonlinear because the conditional probabilities have the probability of the assumption in the denominator rather than the numerator, so you can't simply add the possibilities in any way.

The word term in the previous paragraph is therefore incorrect.

How and why 1/3 gets enhanced to nearly 1/2

If you were only told that "one of the kids is a boy", the mixed families would be overrepresented over the two-boy families by the 2-to-1 ratio because boy-girl and girl-boy families are as likely as boy-boy families; again, the kids notation is younger-older.

However, if you're told that "one of the kids is a Tuesday boy", this overrepresentation almost disappears. Why? Because 1/7 of the boy-girl and girl-boy families have a Tuesday boy. But (approximately) 2/7 of the boy-boy families have at least one Tuesday boy because each of these two boys has a chance to be born on Tuesday.

In this way, the boy-boy families (nearly) compensate the factor of two by which they were underrepresented relatively to the mixed families.

---

Bonus: this puzzle and crackpot Sean Carroll's misunderstanding of logic

This logical puzzle is actually a very precise pedagogical example showing what's wrong with the thinking of various people about the arrow of time. Some people - those who say that the information about Tuesday doesn't matter and who typically end up with the result 1/3 - think that

Prob(cond,any_day) = Prob(cond,Monday) + ... + Prob(cond,Sunday)

where "cond" is an extra condition. So if we make a statement about a specific object and if this statement doesn't prefer any day of the week, then adding the information about "its" day of the week doesn't matter. It only reduces the probability by a factor of 7 if the probability is day-blind.

That's right for "conclusions" or "outcomes". However, the error that these people are making is that they think that this "additive" counting of the probabilities also holds for the probabilities of assumptions, i.e. probabilities of conditions in the conditional probability. But no such a linearity exists over there. Conditions (and initial states) don't follow the same maths as the outcomes (and final states)!

There is no condition-outcome or past-future symmetry in mathematical logic! That's why it matters for the probabilities whether the information about Tuesday is specified even though there is nothing special about Tuesday.

Cat: testing string theory

Via Mike the Technobuddhist and Andy XL who proposes to treat string theory with the respect it deserves.

Amen to that.

Nuclear explosion in Krkonoše

Those who watched a Czech public TV channel in the morning could have seen a nuclear explosion in the Krkonoše Mountains during an otherwise boring breakfast program that normally shows weather at different places, especially touristic targets in the mountains.

See the video (or YouTube I, II)

Who was behind it? No, it wasn't Putin. It was an artistic group called Ztohoven which means "away out of it" but it also sounds identical to the phrase "one hundred excrements". Most likely, Roman Týc was the main spiritual father. This time, they hacked a web camera. But they have already produced several practical jokes of this kind in the past, usually featuring a question mark that complains about the ability of media and commercials to manipulate people.

For example, ex-president Havel used to place a huge heartsuit at the Prague Castle. While some people thought that the Prague Castle became a whorehouse, Ztohoven hid one-half of it the heartsuit that it was changed into a question mark.

While the Czech TV wants to sue them, I tend to agree with some commenters that similar events are probably necessary to teach people how to doubt and rationally think about the news in the media.

And that's the memo.




Start Zwentendorf: nuclear power plants

Karel Schwarzenberg, the Czech minister of foreign affairs, argued in an interview for Austrian press that attacks against the Czechs have become a national sport of Austria. He said that the people who protest the Czech nuclear power plant are morons and that Temelín is safer than many German nuclear power plants simply because it is newer.



Meanwhile, the Austrian "Stop Temelín" organization that has been organizing blockades of the borders has a new sister organization. It is called "Start Zwentendorf". :-) You can check that it is a sister organization by comparing its logo with the logo of the Austrian movement.

The Czech activists demand that the Austrian government protects the environment from pollutants produced by coal burning by a quick launch of the Zwentendorf nuclear power plant, 40 kilometers from the Czech border, which was terminated by 50.4 percent of the voters in a 1978 referendum. They will also be blocking the borders, using similar yellow costumes as their Austrian friends.

The treaty about the new plant should be signed in Melk, just like the treaties about Temelín, to make the place easier to memorize. Once Zwentendorf is running, the "Start Zwentendorf" movement will cease to exist and its agenda will be transferred to a new organization called "Start Zwentendorf block II". :-)

This humor is not new. A Czech anti-nuclear movement was emotionally called "Southern Bohemian Mothers": Temelín is located in Southern Bohemia. Another, pro-nuclear organization called "Southern Bohemian Daddies" was established soon afterwards. ;-)

String Ducky wins 2-minute video contest

The viewers of String Theory in Two Minutes video contest have chosen the Watson family but Brian Greene had a different winner, namely String Ducky. Congratulations!

Hunt for the Higgs boson

Fullscreen. Via JoAnne Hewett.

NYT about Cimrman: memo from Plzeň

The New York Times have an article about Mr Jára da Cimrman. The article about the greatest Czech of all time who has made his greatest achievements at the beginning of the 20th century is titled a "memo from Pilsen" which is my hometown where I will return in July.



Cimrman was born around 1870 in Vienna and he became the greatest playwright, poet, composer, teacher, traveller, philosopher, inventor, detective, and athlete of his era. An asteroid is named 7796 Jaracimrman and hundreds of places in the Czech Republic remember the moments when Cimrman visited them.



Zdeněk Svěrák (left) and Ladislav Smoljak (right) have been two leading historians who have studied Cimrman for decades: they are still the supreme cimrmanologists. More precisely, they became the founders of the Theater of Jára da Cimrman. Their humor is a wise and fine brand of Czech humor even though I find the NYT's description of their humor as "anti-communist sarcasm" to be somewhat misleading because I think it has mostly been apolitical humor.

While it seems rather likely that Jára da Cimrman has never existed, which is why he was disqualified in 2005 from the "Greatest Czech contest" even though he has otherwise clearly won it :-), let me admit that there exist rumors that either Václav Klaus or your humble correspondent might be Jára da Cimrman, after all. But for obvious reasons, I can neither confirm nor deny these rumors.

And that's the memo from Pilsen.

Icon's story

When you go to bed at night and forget to shut down your computer, I think you ought to know what actually goes on. It's 2 AM and do you know where your icons are and what they are doing? Click on this site and you will see what happens when you leave the computer on during the night. Turn up sound and click here!

Map: we know your location

The Reference Frame knows where you are. Please feel free to bookmark this page or link to it if you find it useful. Feel free to drag the map, zoom it in, zoom it out, and so on.




(C) 2007 Luboš Motl, KGB, StB, CIA, FBI, MI5, Google Maps, Microsoft

NetDisaster.COM

If your speakers don't produce a huge amount of noise and if there are no Reference Frame protestors with banners walking across your screen, it is because you haven't yet clicked at this NetDisaster.COM link.

Happy Easter

Full screen

Lidice: total burn-out

This game created by the director of the Lidice Memorial, Milouš Červencl,

• Total Burn-Out (backup)

was rather successful in explaining the world audiences what catastrophes occurred in the Czech village (map) back in 1942. Nevertheless, it was still too sensitive an issue for those who really remember the events and the game had to be removed from the main page of the server...




The game has nevertheless won an international award, Epica Bronze Finalist.

See also: a newer article about Lidice.

How to get from Cambridge to Prague

Google directions will tell you. Let me be brief:

• Head northeast on River Street toward Green Street, 46 feet
• Sharp left at Western Avenue, 0.7 miles
• ... exit, toll road, ...
• Turn right at Long Wharf, 0.1 miles
• Swim accross the Atlantic Ocean, 3462 miles
• Slight right at E05, 0.5 miles
• ... toll road, Amiens, Paris, Pilsen ...
• Turn left to stay on the Wenceslaus Square, 92 feet
  

As you can see, it's not hard to get there. Google estimates that the swimming will consume 30 days. This simple algorithm is the essence of what Sabine calls Transatlanticism. :-)



The picture was taken in October 1998 and Hillary had a good justification for such fun in front of Václav Havel's residence. :-) Besides Transatlanticism, there also exists Transmesopotamism. Two brothers blogging from Baghdad were quoted in a speech by Bush: Iraq the Model. Congratulations.

Swimming: via Backreaction.