This text uses Techexplorer to display math formulae. You may download it but I doubt that it is worth the hassle just in order to see a few cheap formulae in this text.Superstring theory, according to the conventional wisdom, predicts 10 spacetime dimensions. M-theory, its special state, predicts 11. If it describes the real world, 6 or 7 dimensions must be hidden in one way or another. The simplest way to hide them is compactification: the extra 6 or 7 coordinates parameterize a compact shape (a manifold). The simplest compactification is toroidal compactification where you make the coordinates periodic.
Such a treatment preserves all supersymmetries of the original spacetime, and it is not realistic at all. What is the second simplest compact manifold onto which string/M-theory may be compactified? It preserves one half of supersymmetries, it has four real dimensions, and it is the third highest peak in the world after Mount Everest and K2 (as Paul Aspinwall explains in his lecture mentioned at the bottom of this text). How does such a K3 look like? You can either wait for Matt Headrick and Toby Wiseman who are finishing a paper describing the numerical simulations of a particular one-dimensional subclass of K3 surfaces, or you can alternatively look at the following picture:
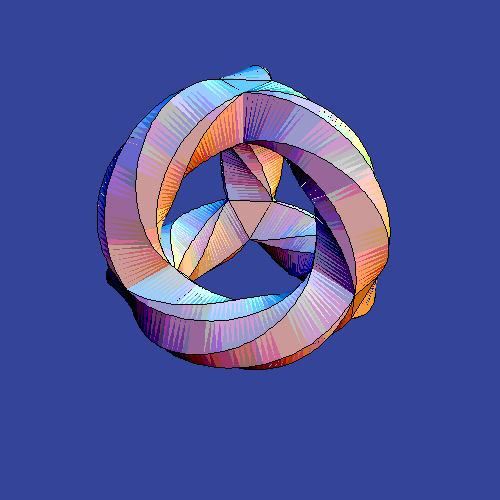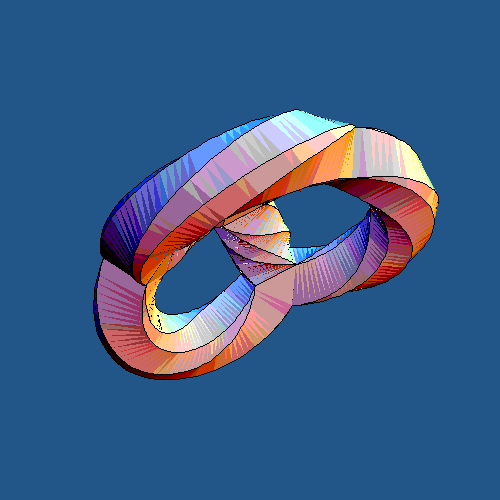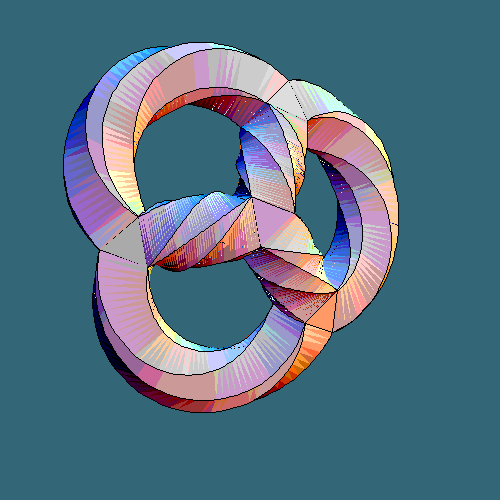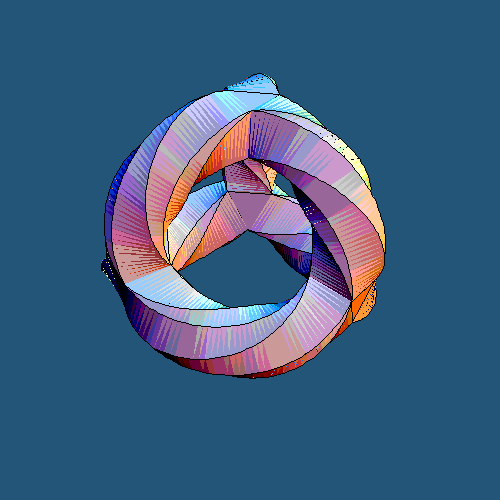
The animation above was created by Greg Egan and promoted by John Baez. It shows you, once again, how the simplest curved compactification of string theory looks like. Well, not quite. Many K3 surfaces may be written as quartic surfaces in the complex projective space CP3 which in homogeneous coordinates means:
These quartic curves are Calabi-Yau spaces for any values of the coefficients "c" (the complex structure moduli) because of the same reason why quintic (5th order) hypersurfaces in CP4 are Calabi-Yaus: the first Chern class vanishes. Because I have not yet installed the higher-dimensional plug-in into my blog, we had to simplify the quartic complex surface a bit. First of all, one of the homogeneous coordinates in CP3 had to be set to zero which means that we really display the intersection of a K3 surface with a hyperplane. The other three coordinates parameterizing a CP2 were reinterpreted as a C2 and another projection from 4 real dimensions to 3 real dimensions was applied in different ways parameterized by "time". The picture above visualizes a particular surface in R3 connected with a particular quartic polynomial (a special choice of the coefficients "c" was made) - a surface of genus 3 which is known as the Klein quartic:
If you're interested about this surface and its symmetries, read
If you're interested in K3 surfaces and the role they play in string theory, start with Paul Aspinwall's lectures